 |
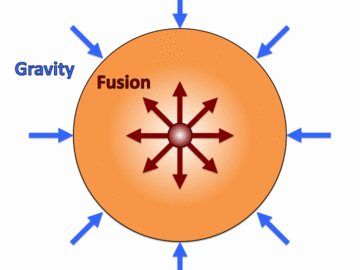
| Fig. 1: Diagram showing the balance of gravitational forces (contraction) with fusion (expansion) that is maintained to keep Sun stable and fusion burning. |
The enormous importance of the Sun is pretty obvious. It is the center of our solar system and keeps all the planets therein confined in its generous gravitational field. [1] It is also the source of energy for life on earth. Nearly all energy can be attributed directly to the sun's rays. These rays are actually photons or particles of electromagnetic radiation which originate at the sun's intensely heated surface and travel through the vacuum of space to Earth's surface. The process which heats the sun is nuclear fusion. This reaction is exemplified in Einstein's famous E=mc2 equation which states that mass can be converted into huge amounts of energy. (the c is the speed of light ~300 million m/s). In nuclear fusion, two atoms must overcome enormous repulsive forces before they can fuse and release massive energy. This requires conditions that are extremely high energy and high density. Thus, the internal temperature of the sun must be kept at nearly 15 million Kelvin. [2]
The fusion process in the sun is a delicate one. This is due to the fact that conditions needed to sustain the fusion burn are very extreme. Indeed, outside of nuclear weapons, fusion has made very few appearances on planet Earth. The burning plasma, or ionized gas, of Hydrogen atoms must be contained, otherwise it will blow apart and decrease its density to a level that will not promote fusion. This occurs in stars when the fusion rate becomes too rapid or the core too hot and the star becomes a supernova. This also is exactly what occurs in an atomic bomb. The "engine" that is the Sun can also go to the other extreme and turn off entirely. If the amount of Hydrogen at the core gets to be too small or the gravity becomes too large, the star can collapse under its own gravity and form a black hole. [3] So how does our sun strike a perfect balance between the explosive forces of fusion and the implosive forces of self gravity?
It would appear that perfectly balancing fusion with gravity would be like balancing an inverted pendulum whilst spinning on a "Merry-go-round." However, the Sun possesses a property which serves as an auto-regulation mechanism for the fusion reaction. [4] That is, the fusion rate will increase or decrease to keep the core temperature at a constant value. To understand this mechanism, we must take a macroscopic view of the Sun. If we assume the Sun is a perfect sphere in hydrostatic equilibrium, we can write down the following equation:
| dP dr |
= | - | G m(r) ρ r2 |
where P is pressure, r is radius, G is the gravitational constant, rho is the density and m is the mass of the sun contained at that radius. This simply comes from Newton's second law of balancing forces and states that pressure will vary based on depth if there is gravity and is trivially derived from the Navier-Stokes equations. [5] The right hand side of the equation is the force of self-gravity. This can be easily seen in a glass of water. The pressure will be higher at the bottom of the glass and decrease as a function of depth till the surface is reached. The same is true of the sun, although the solution is not as trivial this time, as gravitational forces will vary with depth, as will the density. In fact, as is, we cannot solve for the density/pressure profiles of the Sun. We must introduce another assumption to our model and that is an equation of state. This is effectively a relation between thermodynamic variables. In this case, we have a polytropic gas relation given as: [6]
| P | = | K ρ γ |
where K and gamma are constants. This relation gives us a direct relationship between pressure and density and allows us to solve for density and pressure profiles of the sun. The exact profile isn't as important as is trends this model suggests. We also need to assume the ideal gas law is in place which relates temperature to density and pressure. We take a solution to the above equations and then assume the core is over heating and experiencing too much fusion reactions. The core will heat up and the profiles will adjust accordingly, making the core density less. This expansion also decreases the temperature at the core and the fusion reaction rate will decrease.
Furthermore, if the reaction rate of fusion is overly attenuated, the force of gravity will become dominant and the Sun will compress and shrink. This process will increase the core density and cause the temperature to rise, thereby increasing the reaction rate of fusion. Perturbations in either direction of the equilibrium will be neutralized by the Sun's auto-regulation mechanism. This fortuitous balancing act has kept our Sun burning for several billion years and given earth an abundance of energy and life.
© Britton J. Olson. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] M. Woolfson, "The Origin and Evolution of the Solar System," Astron. Geophys. 41, 1.12 (2000).
[2] S. Basu et al., "Fresh Insights on the Structure of the Solar Core," Astrophys. J. 699, 1403 (2009).
[3] S. Chandrasekhar, "The Maximum Mass of Ideal White Dwarfs," Astrophys. J. 74, 81 (1931).
[4] H. J. Haubold and A. M. Mathai, "Solar Nuclear Energy Generation and the Chlorine Solar Neutrino Experiment," Am. Inst. Phys. Conf. Proc. 320, 102 (1994).
[5] G. K. Batchelor, An Introduction to Fluid Dynamics (Cambridge U. Press, 1967).
[6] G. P. Horedt, Polytropes: Applications in Astrophysics and Related Fields (Kluwer, 2004), pp. 8-11.