
 |
| Fig. 1: Rudolph Mössbauer. (Source: Wikimedia Commons) |
The Mössbauer effect is a phenomenon related to the emission and resonant absorption of gamma radiation by certain atomic nuclei fixed in crystal lattices under specific conditions, such that the emission and absorption are essentially recoilless from an internal-energy perspective. [1,2] In fact, the effect is also often referred to as recoilless nuclear resonance absorption, although this is somewhat of a misnomer, as we will see.
The discovery and initial proof of the Mössbauer effect were published in 1958 by Rudolph Mössbauer (pictured in Fig. 1), and led to his winning the Nobel Prize for physics in 1961 at the age of 32. [3] The experimental demonstration of the effect was via a form of spectroscopy (now referred to Mössbauer spectroscopy); the fine precision of Mössbauer spectroscopy has led to limited but specific applications in the study of relativistic effects, lattice structure dynamics, metallurgy, and hyperfine interactions in solids. [4]
Mössbauer's work built upon prior discoveries demonstrating resonant absorption for both electromagnetic and nuclear radiation. Stokes in the 19th century first demonstrated the phenomenon of flourescence, in which solids, liquids, or gases under certain conditions may absorb and re-emit electromagnetic radiation; in the case of resonant flourescence, the emitted and absorbed radiation are of the same wavelength. [1] To build to an understanding of these phenomena, we must speak of the atoms or nuclei in the emitting/absorbing materials as having distinct energy states or levels. An atom in an excited state may emit radiation and in doing so be reduced to its lower energy or ground state; correspondingly, a ground state atom which absorbs radiation of the appropriate energy may transition to its excited state. [1,2] In the optical case, the newly excited atoms having absorbed the radiation will then re-emit that radiation in the form of light, until returning to their lower energy ground states. [1] This was demonstrated by Stokes in his work with sodium bulbs, which emit yellow light when the sodium gas is excited. [3]
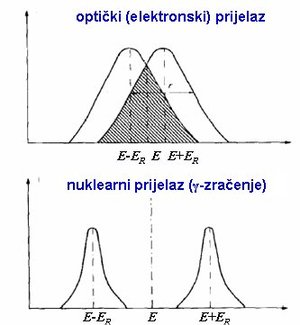 |
| Fig. 2: Emission and absorption lines for optical (upper plot) and nuclear (lower plot) photons. Note the overlap in the optical case, demonstrating the relative ease of achieving resonant absorption. (Source: Wikimedia Commons) |
It is important to note that the energy level of the radiation emitted during a state transition is different from material to material; this is a specific material characteristic. Correspondingly, only radiation of a certain energy level may excite an atom of a given material to a higher energy state; other radiation will pass through or be scattered by the material. [5] This is a probabilistic effect, and so the likelihood of the absorption or emission of radiation can be plotted as a bell-curve with a peak centered at the most likely energy level of emission or absorption. [1] The relative width of this curve is referred to as the spectral linewidth. The linewidths for gamma radiation are much narrower than those for optical radiation. [3]
Using this concept of linewidth, we can develop a condition for the occurrence of resonant absorption; but first, we must develop the idea of recoil when speaking of emission or absorption. Throughout the duration of this review, we speak of a free nucleus as one treated as its own independent energetic system; in this simplified case there are no interactions with neighboring particles unless explicitly stated. [2] Although the theoretical derivations supporting Mössbauer effect are based in quantum mechanics, recoil is easily understood from a classical physical background: conservation of momentum requires that in order for a free nucleus to emit or absorb radiation of non-zero energy, it must itself undergo a change in internal energy, such that the total energy of the system remains constant. [2,5] Emission therefore corresponds to a reduction in energy of the emitting nucleus, and absorption to a gain in energy.
Returning to the concept of linewidths, we can now state our condition for resonance between an emitter and an absorber. Consider a pair of free nuclei (denoted A, B) each with a baseline energy E0. If A emits a phonon, then its energy after emission will be E0 - Er, where Er denotes the associated recoil energy. Then if B absorbs the emitted phonon, its energy after absorption will correspondingly be E0 + Er. The emission and absorption lines will then be bell-curves centered at the points (E0 - Er) and (E0 + Er), with linewidths determined by the material in question as well as the type of phonon emitted. Fig. 2 shows emission and absorption lines for an optical phonon (upper plot) and a gamma phonon (lower plot); the condition for resonance is simply that the two emission lines overlap. [1] The energy not lost to recoil is carried from emitter to absorber via the emitted/absorbed phonon: the overlap implies that sufficient energy may be carried from one to the other to excite the absorber and produce resonance. [1,2,5]
From Fig. 2 we can see immediately why optical resonance is so much easier to achieve than nuclear resonance: the optical linewidths are much wider relative to the recoil energy, and so the overlap condition is much more probable. The characteristic linewidths of gamma radiation are extremely narrow, and so to achieve resonance in free nuclei requires considerable experimental effort to modulate the energies of the system and allow for energetic overlap with any non-negligible probability. As a qualitative example, the isotope Fe-57 (a radioactive decay product of Co-57) may emit a gamma particle; the emission linewidth of 4.47 × 10-9 eV is extremely small compared to the recoil energy of 2.0 × 10-3 eV. [5]
Prior to Mössbauer's work, Moon in 1951 was able to achieve nuclear resonant absorption in free nuclei via the Doppler effect. [1] His experimental setup involved moving the radioactive source towards the absorber in order to shift the emission line and achieve overlap. [1] However, the relatively high velocities needed to succeed required experimental conditions described by Principi as extreme; such a setup was not necessarily practical to build further work upon. [3]
Before introducing Mössbauer's work leading up to the Nobel Prize, we remind the reader that the effects were dealing with are quantum in nature; thus rather than dealing with direct classical solutions to the resonance condition, we are speaking in terms of probabilities of various events. Mössbauer's contribution can then be described in two parts: first, the theoretical demonstration of the possibility of nuclear resonant absorption under less-extreme conditions than as demonstrated by Moon; and second, an experimental demonstration which achieves the theorized effect.
The recoil energy term E_r has an inverse relationship with the mass m of the emitting or absorbing nucleus. [2] Mössbauers premise, simply stated, was that by binding the nuclei in a crystal lattice, one could treat the recoil energy as being applied to the entire lattice mass M >> m, greatly reducing the Er term and allowing nearly all energy to be carried from emitter to absoper via the gamma phonon. [1,2,4] From a more accurate quantum perspective, he theorized that given this lattice binding, there was a non-negligible probability of all recoil momentum being transmitted to the crystal mass M, with essentially zero change to the internal energy of the single emitting or absorbing nucleus; then all energy would be carried from A to B via the gamma phonon and nuclear resonant absorption could theoretically be achieved. [1,2] We will not step through the relevant derivation here, but instead refer the reader to Eyges's excellent paper for a deeper look at the quantum theory involved. [2]
To demonstrate the Mössbauer effect in practice, Mössbauer set up a spectroscopy experiment using Ir-191 as his source/absorber isotope. He also made use of the Doppler effect to precisely line up emission and absorption lines, but with relative velocities between source and absorber on the order of centimeters per second; these experimental conditions were much more practical than those required in Moon's work. [1] The actuator used to move the source was a turntable built using parts from German mechanical toy shops in Heidelberg. [1] Thus the energy of the gamma emission was modulated in small but precisely known amounts. A detector downstream of the absorber would detect the emitted gamma radiation except for at the instant that the resonant absorption condition was achieved; thus a plot of detected gamma radiation vs source velocity would show a relatively constant level of gamma radiation detected with a narrow dip where the absorption occurred. [6]
The proof of concept of Mössbauer spectroscopy generated excitement in the decades following the initial work because of the very narrow conditions for resonant absorption coupled with the very small energetic perturbations necessary to create or destroy said resonant absorption conditions. [4] These characteristics meant that Mössbauer spectroscopy might be used to detect and quantify energetic perturbations of extremely small magnitudes. [3,4]
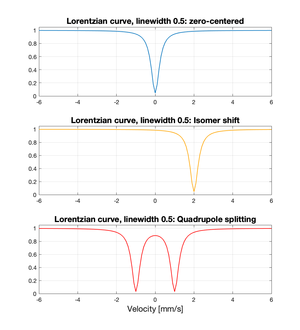 |
| Fig. 3: Sample Lorentzian curves showing the shape of a standard Mössbauer spectrum, as well as with isomer shift or quadrupole splitting. (Source: S. Spaugh) |
In the years following Mössbauer's discovery, a niche set of applications for Mössbauer spectroscopy in physics and materials research have been developed. The precision of this spectroscopy method (due to the narrow width of gamma ray spectral lines) led to some interest developing in the 1960s and 70s towards applications in the study of relativistic effects and the effects of Earth's gravitational field on emitted photons. [4]
A subset of applications are found in the fields of mineralogy, metallurgy and research related to lattice dynamics and hyperfine interactions in solids. [3,4,6,7] Mössbauer spectroscopy is in particular well-suited to the measurement of hyperfine parameters, which describe interactions between particles within an ordered solid. [3] These hyperfine interactions include
Isomer shift, or the electrostatic interaction between nuclear charge densities and electronic charge densities within a solid; this leads to a shift in the Mössbauer spectrum away from zero on the horizontal axis. [3,6]
Quadrupole splitting, or the asymmetrical distribution of electrical charge within a material; this leads to a corresponding split of the Mössbauer spectrum from one negative 'peak' to two. [3,6]
Magnetic splitting, wherein magnetism in magnetically ordered solids splits the nuclear energy levels into distinct peaks; this causes splitting of the spectrum into multiple peaks.[3,6,7]
Mössbauer spectra generally follow the shape of a Lorentzian curve, and so this curve is frequently used for data-fitting purposes, along with the Voigtian (a convolution of the Lorentzian shape with a Gaussian).[8] Sample Lorentzian curves are shown in Figure 3 to demonstrate the shape of an idealized Mössbauer spectrum; the upper plot shows as reference the curve shape without perturbation, while the lower two show how the curve is shifted or split when isomer shift or quadrupole splitting are present, respectively.
Although Mössbauer's initial experiments were carried out using Ir-191 as the emitting and absorbing material, later work trended towards Fe-57 as the isotope of choice; in fact, studies using Fe-57 make up more than 95% of Mössbauer experiments in the field of mineralogy. [3,6] Principi notes that there are 80 isotopes for which a Mössbauer effect is theoretically measurable, but only a few occur in conditions practical for experimental use. [3]
Ninio in 1973 described how in theory the Mössbauer recoilless effect could be achieved in forced harmonic oscillators, via an external energy impulse applied to a lattice structure without changing the internal energy of the lattice, but no experimental work is described in the paper. [9]
Although the practical use cases for Mössbauer spectroscopy are rather limited, it does find application in a small number of research topics, particularly in relation to material interactions at the atomic level. Beyond this, the Mössbauer effect is interesting as a case study in the practical realization of quantum mechanical principles.
© Sarah Spaugh. The author warrants that the work is the author's own and that Stanford University provided no input other than typesetting and referencing guidelines. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] R. Mössbauer, "Recoilless Nuclear Resonance Absorption of Gamma Radiation," in Nobel Lectures, Physics 1942-1962 (Elsevier, 1964).
[2] L. Eyges, "Physics of the Mössbauer Effect," Am. J. Phys. 33, 790 (1965).
[3] G. Principi, "The Mössbauer Effect: A Romantic Scientific Page," Metals 10, 992 (2020).
[4] G. K. Wertheim, "Mössbauer Effect," Physics Today 20, No. 7, 31 (1967).
[5] G. Vandegrift and B. Fultz, "The Mössbauer Effect Explained," Am. J. Phys. 66, 593 (1998).
[6] C. A. McCammon, "Mössbauer Spectroscopy: Applications," in Spectroscopic Methods in Mineralogy, ed. by A. Beran and E. Libowitzky (Mineralogical Society of Great Britain and Ireland, 2004).
[7] G. K. Wertheim, "Mössbauer Effect: Applications to Magnetism," J. Appl. Phys. 32, S110 (1961).
[8] E. Murad, "Developments in Clay Science: Chapter 2.1 - Mössbauer Spectroscopy," Developments in Clay Science 5, pp 11-24 (2013).
[9] F. Ninio, "The Forced Harmonic Oscillator and the Zero-Phonon Transition of the Mössbauer Effect," Am. J. Phys. 41, 648 (1973).