 |
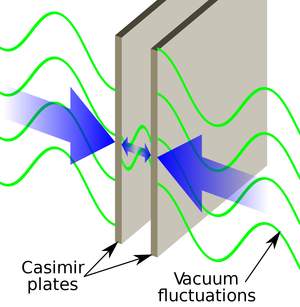
| Fig. 1: Demonstration of the force resulting from discrepancies in the energies of vacuum states, and thus pressure exerted on boundaries. (Source: Wikimedia Commons) |
From the fictional universe of Stargate Atlantis and Marvel Comic's Realm of Kings to NASA's Eagleworks Propulsion laboratory, zero-point energy, also known as vacuum energy, is touted as a potentially limitless and ubiquitous source of energy, if one can only find the means to harness it. [1] Zero-point energy can be formulated in a few different ways, but in its most basic form, it is the minimal yet non-zero energy of a quantum mechanical system. In quantum field theory, zero-point energy can be considered by computing the expected energy of the zero photon mode. [2] In a system with no physical boundaries, the expected energy of the zero photon mode diverges! Yet, if this energy uniformly permeates all of space-time, it is not directly observable.
For pedagogical reasons, we will consider the popular formulation of zero-point energy. The most interesting and relevant framework for zero-point energy can be understood from the quantum field theory for photons and electrons: quantum electrodynamics. Glossing over an exceptional amount of mathematical and conceptual background, the energy of a state in quantum field theory is computed as an expectation of a Hamiltonian, <H>, which describes the energy of the state in terms of operators acting on wavefunctions. The final computation usually requires an integral over the allowed momenta of particles in the state.
Following Schwartz, we can compute the energy of a zero-photon vacuum state with infinite boundaries, a system that is in no way physical, realizable or complete in it's description, but pedagogical nonetheless. [2] Again glossing over much of the background information (which we encourage the interested reader to peruse in reference [2]), we find that, Evac = <H> ∝ ∫ k3 dk → ∞. And thus we see that the expected energy of the vacuum state diverges! Of course this isn't truly a physical system as no other particles are present and there are no boundaries, but it illustrates the idea of energy present in empty space.
A Dutch physicist by the name of Hendrik Casimir took this formalism even farther and considered a slightly more physical system consisting of a conducting and hollow cube of side length L in vacuum. [3] Within this cube is a conducting square plate of side length L, parallel, and positioned in close proximity, to one of the sides of the cube. He then computed two energies: the energy of the zero-photon state, or electromagnetic vacuum state, in the region bounded by the two closely separated planes; and the energy of the vacuum state in the rest of the cube. The two quantities are different as the boundary conditions only allow certain modes, or standing waves, to exist in either region.
Formally, both energies are divergent, yet the difference between the two expressions is well-defined and can be manipulated to compute a force. Casimir interpreted this as an interaction between the closely separated plates and found that there is an attractive force that falls off sharply with separation. A cross-section of the geometry of the two plates and the resulting force is illustrated in Fig 1., where the force is given by the rather simple expression, F = (π2ℏc/240a4) L2 for some separation a. Although the effect is exceptionally small, he predicted "an experimental confirmation seems not unfeasible and might be of a certain interest". [3]
This calculation ignores a significant number of things, such as physical properties of the metals constituting Casimir's box. However, different materials, either metal or non-metal, simply change the coefficient of the computed force, while the dependence on separation and surface area remain the same.
So we've seen that there is a reasonable theoretical framework for the energy associated to electromagnetic vacuum states, and that certain electrode geometries can provide indirect means to observe these vacuum energies. One then might ask, has such a thing been experimentally verified. Although there was a dedicated measurement in 1958 by M. J. Sparnaay, he only found that his measurements did not contradict Casimir's prediction, and indeed they were far from precise. [4]
More recently, circa 1997, a physicist at the University of Washington made use of a torsion pendulum to measure the force been two conductors: one flat and the other hemispherical. [5] He found that at separations of less than 1 micron, there was a comparatively substantial force between the plates that was most readily explained by Casimir's predicted interaction. He took into account modifications to the force from the differing geometry, finite conductivity of real metals, and backgrounds due to both thermal and electrostatic effects. This was the first direct observation and statistically sound analysis to verify the force which Casimir had postulated almost 50 years before.
Since 1997, there has been a wealth of work dedicated to constraining some of the finer and more finicky details of the Casimir effect, as well as studies that have observed other phenomenon associated to vacuum energy, oft referred to as corollaries of the original Casimir effect. The interested reader might try investigating the plasma model vs. the Drude model or the Dynamical Casimir Effect.
 |
| Fig. 2: Photograph of the thruster cavity (copper, left), its supporting structure and enclosing vacuum chamber (rear). (Source: Wikimedia Commons) |
Measuring a force between two metal plates is all well and good (exceptional in fact), but the pragmatist might wonder what use could come of said measurement, or even the applicability of the driving theory itself. With this line of thinking, we finally return to our first reference: an alleged measurement of thrust from a "Casimir Rocket" at NASA's Eagleworks Laboratories. [1] By investigating the relatively new realm of observable consequences of quantum vacuum fluctuations, and making use of highly-skilled space-flight engineers, NASA hopes to construct a propulsion system that does not require a fuel, only energy in the form of electrical power.
To power rockets and provide thrust, current space-flight technologies depend almost entirely on the use of chemicals as fuels, including liquid oxygen, hydrazine, composite solid fuels, and many more. The most significant disadvantage of such a fuel is the fixed thrust to weight ratio. If you want more thrust, or thrust for a longer period of time, you need to bring more fuel. It would be much nicer if you could bring along a little solar-powered space engine, of fixed weight, and get it to push your spaceship around. But what would provide the thrust?
NASA's answer: quantum vacuum fluctuations. And thus Eagleworks was born. Their aim is to make use of complex and highly-specialized conducting cavities to generate a thrust that "pushes" against the vacuum of space by directing the flow of virtual electrons and positrons generated from a standing radio-frequency wave inside the closed cavity. If this were possible, all it would need is a little electricity and the only barrier between humankind and a future in the stars would be the time it takes to get anywhere.
In fact, Eagleworks has recently published a paper detailing a supposed, and exceedingly contentious, measurement of thrust from a prototype Electromagnetic (EM) Drive, depicted in Fig. 2. [1] Their initial 2014 test was not performed in vacuum, which led a number of opponents to claim the thrust was likely due to convection of heat induced by the source of the electromagnetic driving field. However, their recent publication involves a more precise measurement performed in vacuum, which can often be decidedly more conclusive. As with the Great Superluminal Scare of 2011, NASA's result requires extensive scrutiny and where possible, reproduction.
As was mentioned before, this measurement of thrust generated by pushing against the vacuum of spacetime has significant opposition from the physics community, and rightly so. The most obvious issue is a simple violation of conservation of momentum. NASA has claimed to build a "thruster" which, in theory, can propel itself from rest without ejecting either matter or photons. Trivially, pfinal ≠ pinitial which is a problem! Although unlikely, it is possible that the drive is generating thrust by ejecting some other type of weakly-interacting particle, maybe even through a mechanism not currently encoded by the Standard Model.
All physical arguments aside, the measurement claimed supposedly observes a thrust of 10s of micro-Newtons, with a slow (1/f) drift on the order of 100s of micro-Newtons. [1] Purely from a metrological standpoint, this type of measurement is fraught with error, even using techniques to identify signals by their spectral properties. In time, it's possible that better measurements could be made.
Harnessing energy and thrust from the vacuum of space would be undeniably astounding, and is the main project goal at NASA's Eagleworks labs. Yet, such an idea must contend with physical laws like simple conservation of momentum and would benefit from a well-described mechanism, even if it's only an effective description.
Recently in 2017, vacuum fluctuations have allegedly been demonstrated to provide thrust in a prototype EM drive. This is preposterous measurement that is is physically impossible, both from fundamental arguments and a metrological standpoint, as the brief discussion above demonstrated.
© Chas Blakemore. The author warrants that the work is the author's own and that Stanford University provided no input other than typesetting and referencing guidelines. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] H. White et al., "Measurement of Impulsive Thrust from a Closed Radio-Frequency Cavity in Vacuum," J. Propul. Power 33, 830 (2017).
[2] M. D. Schwartz, Quantum Field Theory and The Standard Model (Cambridge University Press, 2013).
[3] H. B. G. Casimir, "On the Attraction Between Two Perfectly Conducting Plates," Kon. Ned. Akad. Wetensch. Proc. 51, 793 (1948).
[4] M. J. Sparnaay, "Measurements of the Attractive Forces Between Flat Plates," Physica 24, 751 (1958).
[5] S. K. Lamoreaux, "Demonstration of the Casimir Force in the 0.6 to 6 μm Range," Phys. Rev. Lett. 78, 5 (1997).