Scaling up the Sublimation Heat Engine

Motivation

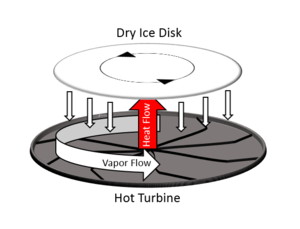
Fig. 1: Heat flow and vapor flow in the sublimation heat engine, after Wells et al. [1]

In order to build a self-sustaining colony on Mars, we will need to develop technology for harvesting energy from locally available resources. In this report we examine a recently proposed heat engine that converts heat to mechanical work through the sublimation of a solid. [1] Evidence exists to suggest that the sublimation of dry ice occurs naturally on Mars due to seasonal temperature variations. [2] Hence, it is plausible that the sublimation heat engine is a viable option for sustaining the energetic needs of human life.

Overview

The prototype demonstrated Wells et al. produced 20 μW of power through the rotation of a dry ice disk, 2 cm in diameter, over a turbine heated to 500°C. [1] In order to make the sublimation heat engine a practical reality, it must be scaled up to larger dimensions. We will propose a method of linearly scaling the turbine geometry that results in a quadratic scaling of the maximum output power while maintaining a constant energy density of the dry ice. We begin with a qualitative summary of the physics of the sublimation heat engine. We then describe how the engine interfaces to an ideal electromechanical generator and derive a bound on the maximum electrical power that the system can source to a resistive load. We conclude with the proposed scaling of the turbine geometry, and a discussion of the thermodynamic and mechanical variables in the expressions for maximum output power and energy density.

Basics

The sublimation heat engine consists of a disk of dry ice levitating and spinning on top of a hot turbine (Fig. 1). With the turbine temperature above the Leidenfrost point of CO₂, the heat conductively transferred to the dry ice is expended in a phase transition from solid to superheated vapor. This results in a flow of vapor from the disk toward the turbine. When the excess pressure in the vapor layer balances the weight of the disk, levitation occurs. Furthermore, the geometry of the turbine induces an angular flow in the vapor stream. Because of viscous drag between the vapor and the underside of the disk, the disk begins to rotate. An expression is given in [1] for the torque τ_L felt by the disk due to drag with respect to the rotating vapor stream in terms of several parameters. Here we break the parameters down into three categories:

The expression

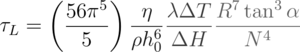
for torque shows that it depends inversely on the thickness of the vapor layer. For a given turbine temperature and geometry, the thickness of the vapor layer is set by the weight of the dry ice disk. A heavier disk results in a thinner vapor layer and a stronger torque. Wells et al. used the criterion for rotation that the thickness of the vapor layer h₀ be of the same order, or larger, than the height of the turbine teeth on the outer rim. [1] Hence, by setting h₀ = (2 π R / N) tan(α), we find the maximum possible torque, which is obtainable using the maximum disk weight permitting rotation. Under these conditions, and assuming that only the mass of the dry ice weighs down on the vapor layer (no additional loads), we have

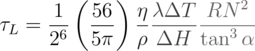
where the height of the turbine teeth H has been expanded in terms N, R, and α.

Disk Drag

Wells et al. reported measurements validating that the acceleration of the disk is consistent with the torque stated above during initial starting of the engine. [1] During this timeframe, the net torque acting on the disk is constant, and its kinetic energy increases quadratically with time. However, the total thermal energy transferred across the vapor layer increases linearly with time. This implies that the disk cannot continue to accelerate indefinitely, and that the net torque on the disk must decrease after some duration of time in order to limit its angular velocity and satisfy conservation of energy. Just as the disk feels a torque due to viscous drag with respect to the rotating vapor below, it also feels a torque due to drag with respect to the stationary air above. The latter drag torque opposes the rotational motion of the disk, and can be derived by integrating the drag force on a differential area element over the total area of the disk. This torque τ_d depends on the density of the air ρ_air, the radius of the disk R, the angular velocity of the rotation ω, and the drag coefficient C_d of the air-disk interface in a rotational situation. We define a drag constant B to simplify the derivations to follow:

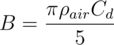
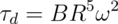
Here we will assume that the air drag on top of the disk limits its angular velocity to stay within a regime in which the fluid dynamics underneath the disk are unaltered. In this manner, τ_L can be considered constant, and the net torque acting on the disk when it spins freely is the sum of τ_L and τ_d.

Electromechanical Generator

We assume that the dry ice disk is coupled to an ideal, lossless electromechanical generator that can be described in terms of a single electromechanical constant. This constant, k_em, is the constant of proportionality between the output voltage and the angular velocity, as well as the constant of proportionality between the back torque and the output current. The constant of proportionality between the output voltage and the output current is simply the load resistance R_L. Using these relations, we can write Newton's second law for the dry ice disk once its angular velocity has reached a steady-state.

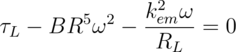
Solving for ω, we find

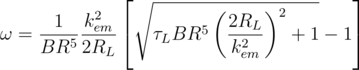
The output power P_out is the product of the output voltage and the output current. In terms of the parameters stated above, the output power is

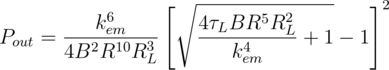
The output power has a maximum with respect to the load resistance. Although the torque due to disk drag τ_d produces a non-linear term in the disk dynamics, the existence of an optimal load resistance is reminiscent of impedance matching in linear systems. The optimal load resistance R_L^* is

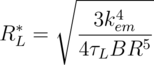
We can think of the optimal load resistance R_L^* as being impedance matched to the mechanical resistance of the disk drag, captured by BR⁵, through the electromechanical transformer that is the ideal generator, captured by k_em. Because the system is non-linear, the impedance match additionally depends on the input torque τ_L. The maximum output power P_out^* is

Scaling

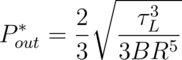
In addition to maximum output power, another variable of interest is the energy density of the dry ice. The energy density captures how much energy can be extracted per unit mass of dry ice, and can be compared against the "mining energy" per unit mass of dry ice. The energy density ρ_E^* is related to the maximum output powe, and the mass flow due to sublimation under matched load conditions:

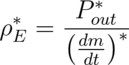
In terms of thermodynamic, mechanical, and geometric parameters, the maximum output power and corresponding energy density are

Using the above expressions for P_out^* and ρ_E^*, we propose that the turbine geometry should be scaled according to the following rule:

• Turbine radius R = kR₀

• Number of turbine teeth N = kN₀

• Height of turbine teeth H = H₀

By scaling the turbine radius and the number of teeth by the same factor, and by keeping the height of the turbine teeth constant, the angle of the turbine teeth remains constant. Scaling according to this rule results in maximum output power growing as k², and energy density remaining constant. Qualitatively, a turbine with a larger radius should have more teeth, but should preserve the tooth size and shape (constant H and α) along the outer rim.

Discussion

In the thermodynamic term, the thermal conductivity and latent heat are physical properties of CO₂. However, the turbine temperature can be adjusted. If the turbine temperature is scaled by some constant k, the maximum output power will scale as k^3/2, whereas the energy density will only scale as k^1/2.

In the mechanical term, the density and dynamic viscosity of the vapor are physical properties of CO₂. However, the drag constant B depends linearly on the density of air ρ_air, which is about 60 times lower on Mars, relative to Earth. Hence, we expect about a factor of 8 improvement in both output power and energy density when operating the sublimation heat engine on the surface of Mars.

In this analysis we assumed that the air drag on top of the rotating disk limits its angular velocity, and that the torque due to the Leidenfrost effect τ_L remains constant up to this limit. The electrical load resistance that maximizes output power in this case is matched to the mechanical resistance of the air drag. Under conditions in which a different dissipative force limits the angular velocity of the disk, rather than air drag, the optimal load resistance may change.

© Danny Bankman. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.

References

[1] G. G. Wells et al., "A Sublimation Heat Engine," Nat. Commun. 6, 6390, (2015).

[2] S. Diniega et al., "A New Dry Hypothesis for the Formation of Martian Linear Gullies," Icarus 225, 526 (2013).