
 |
| Fig. 1: The Neutron Radiography Reactor where its Cherenkov radiation can be observed as a blue glow. (Source: Wikimedia Commons) |
The Cherenkov radiation is analogous with the more well-known sonic boom effect. [1] If an aircraft moves slower than the sound speed in a medium, the air deflection is smooth around the wings of the aircraft. However if the motion speed exceeds the medium sound velocity, then a sudden pressure change would happen and shock waves propagate away from the aircraft in a cone at the speed of sound. [2]
As can be observed form Maxwell's equations for electromagnetic waves, the speed of light in vacuum determined by the constants of permeability and permittivity is the well-known parameter of c (3 × 108 m/s). However the wave velocity in a medium can be changed from the wave velocity in free space due to the polarizability of the material both electrically and magnetically. This so called phase velocity is in fact the velocity at which the phase of photon is propagated within the medium. The ratio of the phase velocity of light in a medium to its velocity in free space is defined as the refractive index n of the material. For most of the materials this is a frequency-dependent parameter and typically a positive number greater than one. When a charged particle is moving faster than light speed inside a medium, a faint radiation would appear which is called Cherenkov radiation, named after Pavel Alexeevich Cherenkov (1904-1990), who studied this phenomenon experimentally in Lebedev Physical Institute of the Russian Academy of Sciences. It is worth mentioning that before Cherenkov, in 1900, Pierre and Marie Curie had observed a blue glow in their experiments with concentrated radium. Following Cherenkov's experiments, in 1937 I. M. Frank and I. E. Tamm gave a classical description of the phenomenon based on Maxwell's equations. Due to their joint work on this radiation phenomenon, in 1958 the Physics Nobel Prize was given to Cherenkov, Frank and Tamm. In what follows we present a brief explanation of the problem followed by its applications in particle physics.
According to classical physics, a moving charged particle emits electromagnetic waves. In a quantum mechanical picture, when a charged particle moves inside a polarizable medium with molecules, it excites the molecules to the higher levels and excited states. Upon returning back to their ground state, the molecules re-emit some photons in the form of electromagnetic radiation. According to the Huygens principle, the emitted waves move out spherically at the phase velocity of the medium. If the particle motion is slow, the radiated waves bunch up slightly in the direction of motion, but they do not cross. However if the particle moves faster than the light speed, the emitted waves add up constructively leading to a coherent radiation at angle θ with respect to the particle direction, known as Cherenkov radiation. The signature of the effect is a cone of emission in the direction of particle motion. Fig. 1 shows a schematic of the Cherenkov radiation showing the typical spherical wavefront and the resultant radiation.
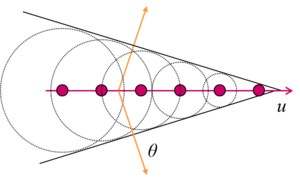 |
| Fig. 2: The schematic of Cherenkov radiation for a particle moving at velocity u. |
For a medium with small refractive index such as gas or water, the minimum speed of particle that would generate a Cherenkov radiation would be a noticeable fraction of c. For example in water where n=1.33, the particle should move at least at the speed of 2.3 ×108 m/s to generate Cherenkov radiation. At these large speeds the particles must be treated relativistically to capture all the effects. Though one can employ classical approaches in denser media as presented in Jackson, here we derive the results for relativistic particles and describe how θ can be determined. [3]
Let us assume that a particle with rest mass m0 and momentum P0 is moving in a medium with refractive index n. Upon its propagation, a photon with momentum Pc = hc/λ, where h is Planck's constant, would be emitted. If the radiated photon makes angle θ with the direction of propagation, then conservation of momentum requires that
Conservation of energy then requires that
where ν = c/(n λ). Solving for θ, we obtain
| cos θ | = | 2 (P02 c2
+ m02 c4)1/2
+ (n2 - 1) hν 2 P0 c n |
In most cases, the second term is negligible, and the angle of the emitted photon can be approximated as cosθ ≅ c/(n u), where
| u | = | β c | = | P0 c2 (P02 c2 + m02 c4)1/2 |
is the particle's relativistic velocity. For relativistic particles, the Cherenkov radiation occurs at a fixed angle. For non-relativistic particles however, the above arguments are not held accurately. There the radiation is mainly caused by the different polarization dipoles of the medium in front and back of the moving particle. It should be mentioned that most materials are dispersive, i.e. their refractive index varies with frequency. Therefore the photons of different energy are scattered in various angles. As for x-rays, the refractive index of typical materials drops below 1, no Cherenkov radiation can be observed within that range.
The number of photons from Cherenkov radiation at a given wavelength and the angle of radiation is given by
| ∂2N ∂x∂λ |
= | 2πα (1 - 1/β2n2) 1/λ2 |
where α=1/137 is the fine structure constant. Unlike the fluorescence or emission spectra, the Cherenkov radiation spectrum given by the above formula, is continuous and its density is inversely related to the wavelength squared. Therefore, the number of photons increases as the wavelength decreases. That explains why most of the Cherenkov radiation seems blue and mostly in UV range. In a nuclear reactor the blue radiation around the reactor is in fact the Cherenkov radiation, where the emitted β particles from the fission lead to the glow. Figure 1 shows the image of a neutron radiography reactor from National Laboratory of Idaho. In the realm of astronomy and cosmology, Cherenkov radiation is produced by charged particles traveling faster than the speed of the light in air. This emission is determined by the value of n, which is proportional to density of the atmosphere.
Integrates the above density within a wavelength range, the number of emitted photons in desired spectral range would be determined by the following equation. This photon number is proportional to the number measured by an intensity detector.
| ∂N ∂x |
= | 2πα (1-1/β2n2) (1/λL-1/λH) |
In particle physics, the Cherenkov radiation is used frequently in particle identification detectors (PID). Particle identification plays a crucial role in particle physics to separate particles such as protons, electrons, muons, pions, etc at different velocities. Cherenkov counters can be categorized to two main types: threshold and imaging counters. Based on the radiated angle equation, if the particle velocity exceeds 1/n, then photons would be generated. This can be set as a threshold measurement mechanism through which the number of particles at given velocity would be determined. By varying the pressure of the gas in a detector, the number of particles passing the threshold velocity changes. Correlating this change to the gas pressure can be used for particle identification. This effect gives a comparative study of the particle speed compared to the phase velocity of light in the medium. Simply by observing the existence of the Cherenkov radiation from a particle, one can determine its relative velocity with respect to the light speed in medium. Knowing that, one can determine the particle momentum. In β-ray detectors one can use a magnet to determine the momentum and direction of motion for a charged particle. [4] Employing the Cherenkov detectors the characterization can be extended to the angular distribution measurement of the scattered particles.
In recent years there have been an increasing interest in synthetic and artificial groups of material known as negative refractive meta-materials. In these materials the phase velocity is opposite to the group velocity direction. Therefore it seems that in such materials the phase propagates backward as the energy propagates in the forward direction. In his theoritical work in 1968, Veselago showed that in these types of materials the Cherenkov radiation would be reversed. [5] The interaction of the charged particle with and its propagation inside such medium leads to the Cherenkov radiation propagating backwardly.
In this report we introduced the Cherenkov radiation phenomenon followed by some qualitative explanations of the phenomenon origin. Using the conservation of momentum and energy the radiated photons and the direction of the Cherenkov radiation were derived for relativistic particles. We continued the report with some of the basics of Cherenkov based PID. Finally we concluded the report with a brief outlook toward the applications of the new generation of artificial negative index materials for the study reversed Cherenkov radiation.
© Hadiseh Alaeian. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] J. V. Jelle, "Cerenkov Radiation and Its Applications," Br. J. Appl. Phys. 6, 277, (1955).
[2] J. D. Anderson, Fundamentals of Aerodynamics, Third Ed. (McGraw-Hill, 1984).
[3] J. D. Jackson, Classical Electrodynamics, Third Ed. (Wiley, 1998).
[4] H. Alaeian, "An Introduction to β-Ray Spectroscopy," Physics 241, Stanford University, Winter 2014.
[5] V. G. Veselago, "The Electrodynamics of Substances With Simultaneously Negative Values of ε and μ," Sov. Phys. Usp. 10, 509 (1968) [Uspek. Fiz. Nauk. 92, 571 (1967)].