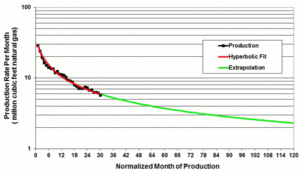
 |
| Fig. 1: Example showing decline curve and extrapolation of decline to estimate recovery. [5] (Courtesy of the U.S. Geological Survey.) |
Hydrocarbon reserve can be defined as those quantities of petroleum anticipated to be commercially recoverable by application of development projects to known accumulations from a given date forward under defined conditions. [1] It is important to differentiate between hydrocarbon reserves and hydrocarbon resources. The latter is roughly defined as sum of recoverable and unrecoverable volumes of hydrocarbon in place. There is always uncertainty in making reserve estimations. The main source of the uncertainty is lack of the geological data (e.g., porosity and permeability) available. Based on the quantity and quality of the available data, different methods for the estimation are used. For example, in the early stage of the hydrocarbon reservoir development, very little information is available; hence, rough estimations are usually done by using analogy or volumetric calculations. Whereas, on the late stage of reservoir development, decline curve analysis and reservoir simulation methods are commonly employed. This paper discusses most commonly used methods for reserve estimation of a given hydrocarbon reservoir.
The most basic technique for the reserve estimation is Volumetric method. It is used to indirectly estimate recoverable volumes from estimates of reservoir volume, porosity, oil saturation, and recovery efficiency. The reserve estimate are obtained using simple volumetric relation:
Here, V is reservoir volume, φ is average porosity, S0 is the average oil saturation, and b0 is oil formation volume factor. Note that here porosity and saturation are estimated (using different sources of information such as well logging, well tests, and seismic data) and have their own uncertainties. Recovery factor is also uncertain and obtained based on rock and fluid properties, reservoir-drive mechanisms, and reservoir geometry. For the traditional deterministic approach the input parameters (e.g., φ, S0, etc) are single-valued, the corresponding reserve volume is also a single-valued "best" estimate. For a modern stochastic approach, the input parameters are represented by means of probability density functions (PDFs), and the resulting reserve estimate is a combination of these PDFs. The PDFs are usually "combined" using Monte Carlo Simulation.
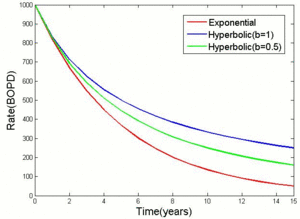 |
| Fig. 2: Hyperbolic and Exponential Decline Curves. |
As hydrocarbon reservoir matures and production data become available, Decline Curve Analysis and Material Balance methods become the predominant methods for estimating reserves. [2] In Decline Curve Analysis production data is extrapolated using semi-empirical equations and reserves are estimated by this extrapolation. Here the main assumption is that the trend established in the past will govern the future in a uniform manner. [3] Therefore, the method should only be applied to the wells with uniform, lengthy production history. Two commonly-used extrapolation formulas for the production rate q(t) are
| Exponential: | q(t) = qi exp(-Dit) | |
|---|---|---|
| Hyperbolic: | q(t) = qi (1+bDit)-1/b |
where qi, Di and b are constants. Fig. 1 shows example of hyperbolic decline curve that is fitted into the production data. Theoretically the method is applicable only to the single well computations; however, in practice, production extrapolations done for a group of wells often provide acceptable approximations. The choice of proper decline equation is essential for the reserve estimation. Fig. 2 demonstrates exponential and hyperbolic decline curves that start with the same initial production. It can be seen that for the first two years all decline curves fit nearly exactly and produce significantly different forecast for the later time. Therefore, the requirement of lengthy uniform decline is fundamentally important for the successful application of the method.
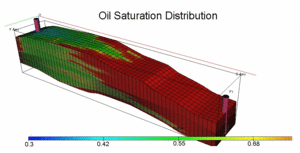 |
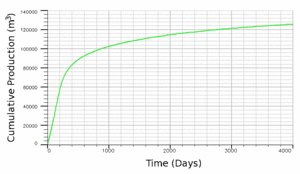 |
| Fig. 3: Example of Reservoir Simulation Results: Oil Saturation Distribution (top) and Cumulative Oil Production Rate (bottom). (Source: R. Zaydullin) |
Another widely used technique for the estimation of recoverable hydrocarbons in place is a Material Balance method. Here the whole reservoir is treated as a closed tank where material (mass) is conserved. The reserve estimate is obtained from the measurements of fluid production and the resulting change in reservoir pressure caused by the production. [2] The fluid properties, production and pressure data are averaged throughout the reservoir and mass conservation equation is solved analytically for the averaged system. The method is more reliable than Volumetric methods as long as there is sufficient data to establish the pressure-hydrocarbon production relationship. [4] As in the case of Volumetric method, Material Balance approach can be used in either deterministic or stochastic fashion.
A natural extension of Material Balance method is numerical Reservoir Simulation. In essence, reservoir simulator is a software that numerically solves mass and energy conservation equations for the whole reservoir that is represented as a 3D grid. Grid blocks usually have non- uniform geologic properties such as porosity and permeability. The fluid flow between different grid blocks is assumed to be governed by Darcy law. Modern reservoir simulators can handle muticomponent, mulitiphase fluids in presence of complex thermal effects. Depending on the problem, imposed grid can vary from 104 to 108 grid blocks. The governing discretized conservation equations are nonlinear; hence, iterations are needed to obtain solution. The grid size and severe nonlinearities affect simulation time significantly; typical simulation time for realistic reservoir model can vary from hours to several days. Common outputs of reservoir simulation modelling are saturation distribution and production curves (Fig. 3). Use of reservoir simulators can significantly enhance understanding of reservoir recovery mechanism and provide good estimation for recovery factor. Reservoir simulation studies are commonly done using stochastic approaches where porosity and permeability distributions are populated using geostatistics methods.
© Rustem Zaydullin. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] "Petroleum Resources Management System," Society of Petroleum Engineers, January 2008.
[2] "Petroleum Reservoir Estimation Methods," Petrobjects, 2004.
[3] F. Demirmen, "Reserves Estimation: The Challenge for the Industry," J. Pet. Technol. 59, No. 5, 80 (2007).
[4] R. Mireault and L. Dean, "Reservoir Engineering for Geologists," Fekete, October 2008.
[5] R. R. Charpentier and T. A. Cook, "Variability of Oil and Gas Productivities for Continuous (Unconventional) Petroleum Accumulations", U.S. Geological Survey, Open File Report 2013-1001, 2013