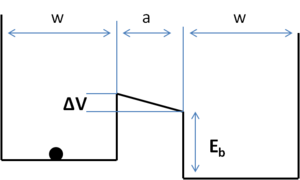
 |
| Fig. 1: Model for a quantum well computation system. |
Gordon Moore had predicted in 1965, that electronic device dimensions will scale following a trend. [1] It is accepted today as the Moore's Law, a rule of thumb, that the number of transistors packed in an Integrated Circuit doubles approximately every 2 years. People innovate to stay ahead of the lot by making devices smaller for several advantages, including packing density. [2]
"Devices" today largely refer to CMOS transistors. "Feature size" today refers to transistor parameters like gate insulator thickness, channel length, etc. or circuit parameters like distance between closest interconnects. Any future electronic device, transistor or not, will see it's limits in the laws discussed here.
To perform useful computation, we need to irreversibly change distinguishable states of memory cell(s). The thermodynamic entropy to change n memory cells within m states is ΔS=kBln(mn), where kB is the Boltzmann constant. From the second law of thermodynamics, ΔS=ΔQ/T, where ΔQ is the energy spent and T is the temperature. So the energy required to write information into one binary memory bit is Ebit= kBT ln2. This is known as the Shannon-von Neumann-Landauer (SNL) expression. This tells us that we need at least 0.017 eV of energy to process a bit at 300 °K.
From Heisenberg's Uncertainty Principle ΔEΔt≥ħ, for Ebit of 0.017eV, the time to switch is atleast 0.04 ps. From ΔxΔp≥ħ or Δx≥ħ/√2mE , the minimum feature size corresponding to an electron as the carrier is 1.5 nm. The power per area, P=n × Ebit/tmin, where n=1/xmin2 is the packing density (~4.7 ×1013devices/cm2), is about 3.7 MW/cm2 (The surface of the Sun is 6000 W/cm2). These are not the limits, yet. In the next section, we will correct these formulas by considering tunneling.
Consider a quantum well system as shown in Fig 1. The probability of thermionic injection of the electron over the barrier height is GT=exp(-Eb/kBT). The probability of tunneling through the barrier is GQ=exp(-2a√2mE /ħ). [3] For the two states to be distinguishable, the limiting case is Gerror=GT+GQ-GTGQ=0.5. Solving, we get Ebmin = kBT ln2 + (ħ ln2)2/(8ma2). The power for an area A having n devices operating at a frequency f is Pmax =f (n/A) [kBT ln2+(ħ ln2)2/(8ma2)].
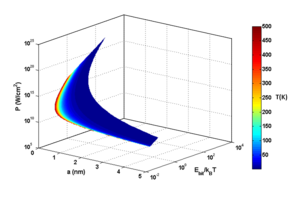 |
| Fig. 2: Plot of energy, Ebit, and power, P, as a function of feature size, a, at different temperatures. |
How much we can allow the power to rise depends on how much rise in temperature the chip can stand (typically upto 400 °K) and on how fast we can remove the heat from the chip. Newton's Law of Cooling governs heat removal as Q = H(TDev - Tsink). H is the heat transfer coefficient, which is determined by the material constants like specific heat, viscosity, thermal conductivity, heat capacity, etc., apart from the geometry of the cooling structure. [4-5]
When TDev < Tsink, it appears from the first section that Ebit gets better. But Carnot's theorem says that the work needed to remove heat Q is W = Q (Tsink - TDev)/TDev. So
| Ebittotal | = Ebit + Ebit (Tsink - TDev)/TDev |
| = kBTsink ln2 + (Tsink/TDev) (ħ ln2)2/(8ma2) |
Ebittotal and power are plotted against a and temperature in Fig. 2.
From Fig. 2, we see that 1) cooling the system does not help Ebit at all, 2) power is ridiculously high for features less than a nanometer and 3) Ebit required is also very high below 2 nm, while it is about kBT ln2 for higher features. Notice that, as we approach smaller features, Ebit and power are far better behaved at higher temperatures than at lower temperatures.
Power consumption and speed are limited fundamentally by the devices, but practically by the electrical parasites, interconnects and chip architecture. This is the reason for the clock speed to have saturated at about 3GHz for today's processors. All alternative ideas, like optical interconnects and more would see their limit in the domain conversion, which is limited by thermodynamics discussed here. The "2" in kBT ln2 can be made higher to, say, m, but that only pushes the limits by a factor of ln(m)/ln2. [6-7]
We will hit these scaling limits in 30-40 years. We do not know if we can compute in other methods that are governed by laws yet to be explored. We are neither sure if we will realize fundamental passive components like memcapacitor and meminductor, which remain fantastic theoretical predictions for computing without power. [8]
© Suhas Kumar. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] G. E. Moore, "Cramming More Components Onto Integrated Circuits," Electronics 38, No. 8, 114 (1965).
[2] C. A. Mack, "Fifty Years of Moore's Law," IEEE Trans. Semicond. Manuf. 24, 202 (2011).
[3] A. P. French and E. F. Taylor, Eds., An Introduction to Quantum Physics (Norton, 1978).
[4] I. Mudawar, "Assessment of High-Heat-Flux Thermal Management Schemes," IEEE Trans. Comp. Packag. Technol. 24, 122 (2001).
[5] C. LaBounty, A. Shakouri, and J. E. Bowers, "Design and Characterization of Thin Film Microcoolers," J. Appl. Phys. 89, 4059 (2001).
[6] L. B. Kish, "End of Moore's Law: Thermal (Noise) Death of Integration in Micro and Nano Electronics," Phys. Lett. A 305, 144 (2002).
[7] V. V. Zhirnov et. al., "Limits to Binary Logic Switch Scaling - A Gedanken Model," Proc. IEEE 91, 1934 (2003).
[8] M. Di Ventra, Y. V. Pershin and L. O. Chua, "Circuit Elements With Memory: Memristors, Memcapacitors, and Meminductors," Proc. IEEE 97, 1717 (2009).