
 |
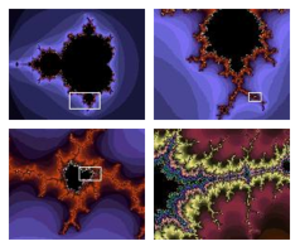
| Fig. 1: Mandelbrot Depiction (Sources: Wikimedia Commons a b c d) |
 |
| Fig. 2: Koch Snowflake pattern, at iteration 0, 1, 2, and 3. |
As the world becomes more and more dependent on cellular devices, there has been an increasing demand in antennas that are compact, conformal, and broadband. [1] A popular method of achieving these characteristics in an antenna is by exploiting the property of fractals. The exploitation of the geometry of fractals in science and engineering has lead to a new field known as fractal-electrodynamics, which has greatly influenced antenna theory. [2] Traditional antenna design has been based on Euclidean geometries, but novel designs have come from modern fractal antenna engineering. [2]
Fractals are difficult to define mathematically, but there are some key features that are generally seen in fractals. Usually, there is some degree of self-similarity in fractals. This means, if a small part of a fractal is magnified, more features that are reminiscent of the whole can be seen. [3] A popular depiction of this is shown in Fig. 1, which is the Mandelbrot set. Fractals also have fractional dimension, and fractals as mathematical equations cannot be measured in traditional ways, meaning they are nowhere differentiable. Another example of a fractal set, is the Koch snowflake. The first few iterations can be seen in Fig. 2.
A fractal antenna uses a self-similar design to maximize the length of a material in a total surface area. This makes fractal antennas compact and wideband. [1] The fractal element of the antenna allows it to have many different resonances, meaning it will act as an antenna for many different electromagnetic frequencies, as can be seen in Fig. 3. The different resonances arise because the fractal nature of the antenna acts as a virtual network of capacitors and inductors. [4] Currently, many cell phones use a Planar Inverted-F Antenna (PIFA), which is small, low-profile, and is sensitive to both horizontal and vertical polarized radio waves. [5] The drawback is it is narrow bandwidth and not multiband. Fractal PIFA has been designed to address these problems, and results are promising. [5]
 |
| Fig. 3: Resonances allowed for this geometry. |
 |
| Fig. 4: Cantor Set F-PIFA Evolution. |
A Fractal PIFA is works similarly to a traditional PIFA, but has fractal design. The design is based on a two dimensional triadic Cantor array. [5] A perfect fractal antenna would be obtained by iterating the simple Cantor array an infinite number of times, but practically, this is only done about two or three times. This simple design can be seen in Fig. 4. This Fractal PIFA design has allowed for a 500 MHz Bandwidth after the third iteration. [5]
Applications for fractal geometries in cellular devices have become hot topics of research in science and engineering because of consumer demand. Fractal antennas take advantage of geometries that cannot be obtained from Euclidean constructs to deliver exactly what consumers need.
© 2012 Ken Ferguson. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] D. H. Werner and S. Ganguly, "An Overview of Fractal Antenna Engineering Research," IEEE Antennas and Propagation Magazine 45, No. 1, 38 (2003).
[2] D. H. Werner, R. L. Haupt and P. L. Werner, "Fractal Antenna Engineering: The Theory and Design of Fractal Antenna Arrays," IEEE Antennas and Propagation Magazine 41, No. 5, 37 (1999).
[3] S. H. Strogatz, Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering (Westview Press, 2000).
[4] C. P. Baliarda, J. Romeu and A. Cardama, "The Koch Monopole: A Small Fractal Antenna," IEEE Trans. Antennas and Propagation 48, 1773 (2000).
[5] N. A. Saidatul et al., "Multiband Fractal Planar Inverted F Antenna (F-PIFA) for Mobile Phone Application," Prog. Electromag. Res. B 14, 127 (2009).