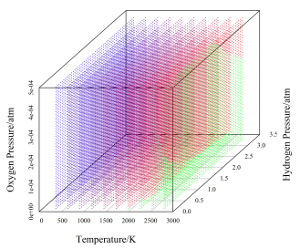
 |
| Fig. 1: Stability window of water under various conditions. |
A hydrogen explosion has been identified as a possible cause of the Chernobyl reactor explosion. [1] A mixture of hydrogen and oxygen under pressure is indeed a very dangerous mixture, so having the means to predict the stability of water under a given set of conditions is important.
The stability of water against decomposition into hydrogen and oxygen can be estimated using the Nernst equation [2]:
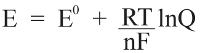
where E0 is the standard potential difference for the transformation, R is the universal gas constant, T is kelvin temperature, n is the number of electrons transferred per reaction, F is the Faraday constant, and Q is the reaction quotient (a measure of the abundance of relevant species to the chemical reaction). The equation takes the partial pressures of relevant gases and concentration of relevant ions as inputs and outputs a potential difference. This potential difference corresponds to a window of stability outside of which water will break down into either oxygen or hydrogen (or both if the two reactions occurring are in electrical contact, as in an electrolyzer for hydrogen generation) according to the following equations:
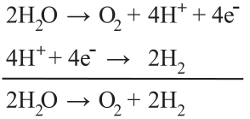
For the Nerstian description of water stability, the relevant species are oxygen, hydrogen. Plugging in the constant values for this reaction yields the relationship:
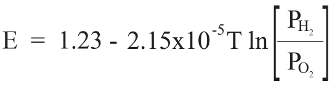
where T = 553 °K, concentration of O2 in solution = 5 ppb, concentration of H2 in solution = 37.5 mL/L H2O, and pH = 6.8.
Unfortunately, in order to apply the Nernst equation, we need to know the partial pressures of oxygen and hydrogen, not the concentration in solution. Since these values are relatively dilute, Henry's law can be used to approximate the partial pressures corresponding to those solubilities, as the following relation [4]:
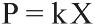
where P is the pressure above the solution, k is the Henry's Law constant for the gas in question, and X is the mole fraction of that gas in solution. Normally Henry's Law constants are only determined under near-room temperature conditions, so high-temperature Henry's Law constants must be determined. Fortunately, the process for estimating the temperature-dependent Henry's Law constant is well-documented in the literature, and relations are readily available for both hydrogen and oxygen. At 553 °K, the "ideal" reactor temperature, the Henry's Law constants for hydrogen and oxygen are 24309.5 atm and 17955.79 atm, respectively. [5] The mole fractions of hydrogen and oxygen can be determined by converting from the given units of concentration:
and the partial pressures of hydrogen and oxygen are readily calculated to be 0.672 atm and 5 × 10-5 atm, respectively. Applying these parameters to the Nernst equation results in a stability window value of 1.107 V. The thermodynamic standard potential window (as defined at pH = 0, all gases at 1 atm, 298 °K) is 1.228 V. Under the above "typical" reactor conditions, water is still relatively stable, suffering a shrinkage of the stability window of only about 10%.
Small perturbations to the typical conditions will not adversely impact the stability of water; however, one can imagine that significant excursions from this regime could result in a serious contraction of the stability window of water. To that end, a plot can be constructed of the "stability space", provided that we hold the system pH constant. This is a valid procedure since the stability window of water is not influenced directly by pH (i.e. water is just as stable at pH 0 as at 14; of course, pH is important with respect to corrosion of core components). The resultant plot is shown below, calculated over the range of partial pressures corresponding to the interval from normal conditions up to conditions where immediate intervention is required (i.e. the conditions bordering on catastrophic failure). [3] The color mapping corresponds to a range of 0 V (red, border of spontaneous dissociation) to 1.23 V (blue, normal stability at room temperature), and regions in green are areas where water will spontaneously dissociate (i.e. the voltage window predicted by the Nernst equation is negative).
It is clear from the plot that water is thermodynamically stable over a wide variety of conditions. Note that the stability window is significantly more sensitive to oxygen pressure than hydrogen pressure in absolute terms. Also note that at approximately 2750 °K the stability window of water has almost completely disappeared, even under relatively high hydrogen and oxygen pressures. The reactor core in the chernobyl disaster has been estimated to have reached this temperature, at least in portions. [6] It is therefore possible that significant hydrogen pressure could have developed during the meltdown, providing additional explosive power for breaching the containment vessel.
© Marie Maher. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] E. M. Pasukhin, "Explosion of Hydrogen-Air Mixture as a Probable Cause of Destruction of the Central Room of the Fourth Block of the Chernobyl NPP as a Result of the Accident on April 26, 1986," Radiochem. 39, 378 (1997).
[2] G. Wulfsburg, Inorganic Chemistry (University Science Books, 2000) p. 264.
[3] W. Bilanin et al., "LWR Water Chemistry Guidelines," Prog. Nucl. Energy 20, 1 (1987).
[4] D. A. McQuarrie and J. D. Simon, Physical Chemistry: A Molecular Approach (University Science books, 1997) p. 979.
[5] K. Watanabe and R. B. Dooley, "Guideline on the Henry's Constant and Vapor-Liquid Distribution Constant for Gases in H2O and D2O at High Temperatures," The International Association for the Properties of Water and Steam, September 2004
[6] L. Devell et al., "Initial Observations of Fallout from the Reactor Accident at Chernobyl," Nature 321, 192 (1986).