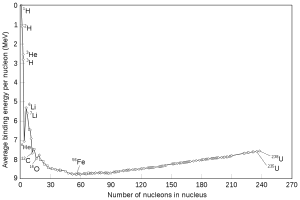
 |
| Fig. 1: Nuclear binding curve. The most stable nuclei lie at the bottom. |
Chemists have long known that it is possible to release large amounts of energy by rearranging atoms – and indeed this is how extract energy from coal, oil, and natural gas. But it was not until the twentieth century that we learned of another process, that of rearranging the protons and neutrons in the atomic nucleus, could release a million times more energy than any chemical process. Because they rearrange atomic nuclei, these processes are called nuclear reactions.
The energy of a nuclear reaction can be calculated using the Nuclear Binding Energy Curve, Fig. 1. This graph quantifies how tightly nuclei are bound together; the greater the binding energy, the more stable and more tightly bound the nucleus. Because of this, it is generally true that light elements can release energy by fusing into heavier elements. Main-sequence stars, for example, burn hydrogen into Helium-4. Most current fusion reactor concepts, by contrast, work by fusing two heavy isotopes of hydrogen – deuterium (D = 2H) and tritium (T = 3H), in what is called the DT Reaction:
This reaction releases a prodigious amount of energy – a single gram of fuel can produce the energy equivalent of 80 tons of TNT. The difficulty lies in getting the fuel to ignite. Naively, one can use basic electrostatics to show that temperatures of hundreds of keV (109–1010 K) are needed to overcome the electrical repulsion between the nuclei; such a requirement would rule out any practical fusion reactor on Earth. However, quantum tunneling allows the reaction to proceed even if the barrier is not fully overcome, and this reduces the required temperature a "mere" 20 keV, i.e. around 200 million K. [1]
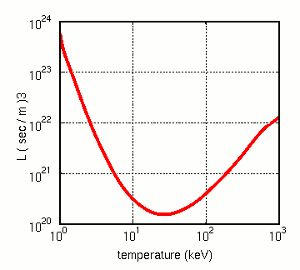 |
| Fig. 2: The Lawson curve (red line) plotted on temperature–nτ space. Ignition occurs for conditions above the line. |
It is not enough, however, to simply start a fusion reaction; one can accomplish this with a tabletop laser apparatus if one likes. In order to break even, a fusion reaction must release more energy than is put into heating up the fuel. This condition is known as ignition, and it has long been known that ignition will occur when the Lawson Criterion is satisfied: [2]
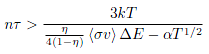
Here n is the particle density of the plasma, τ is the confinement time, and T is the temperature. The other factors on the right hand side (the efficiency parameter η, the average reaction rate ‹σv›, and the bremsstrahlung coefficient α) quantify the balance between the energy entering the plasma through fusion reactions and the energy being radiated away. Using Lawson's choice of variables, we find that
at the optimum temperature of T = 20 keV. Much of the past half-century's research, be it in magnetic tokamaks like JET and its antecedents, or the laser factilities that preceded the NIF, has focused on attempting to achieve conditions that satisfy the Lawson Criterion.
 |
| Fig. 3: Top: The NIF building covers an area of roughly three football fields. Center: NIF laser beam amplifiers. Bottom: NIF ignition chamber. (Courtesy of the Lawrence Livermore National Laboratory.) |
In Inertial Confinement Fusion, a pellet of DT fuel is compressed by a laser to temperatures and densities high enough to satisfy the Lawson criterion. Most inertial confinement methods proceed a three-step process. First, the pellet of DT fuel is heated by the external power source. This heating blows off the outer layers of the pellet, and by Newton's Third Law, compresses the core to 1/1000th of its original volume. The external pulse sends a compressional shockwave to the center the pellet. If the original wave is highly spherical and hydrodynamic instabilities do not disrupt the wave, it will produce extraordinary temperatures and pressures at the center of the pellet. These conditions will be maintained for a time of order
where r is the radius of the compressed fuel pellet and v is the thermal velocity of the ions. Ignition will only take place, of course, if the Lawson Criterion is satisfied, and this leads naturally to the following requirement: [1]
(Here ρ is the compressed pellet mass density and r is is radius). In order to achieve this compression, Keefe (1982) enumerates three conditions that a laser confinement system must satisfy. These conditions give lower limits for the laser's energy, power, and power flux density: [1]
Keefe, it turns out, was a bit too optimistic. More recent simulations indicate that around 2 MJ and 500 TW are needed to ignite the fuel. [3] The NIF is the world's first laser to satisfy these conditions. [4] If ignition succeeds, a thermonuclear burn wave will propgate out from the point of ignition and consume the entire pellet. The gain of a fusion event refers to the ratio of energy out to energy in:
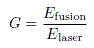
Scientific breakeven is defined as a gain of at least unity; thus far, no ICF facility has achieved scientific breakeven. However, an ICF plant must do much more than break even in order to generate power. Since lasers are very inefficient machines, gains of at least 100 are needed for a plant to produce net power output.
The National Ignition Facility (NIF) is the latest and biggest in a series of lasers built to achieve inertial confinement fusion. Over a decade in the works, it began experiments at full power earlier this year. [4] Although the NIF cost $4 billion to build and covers the area of a typical football stadium, its basic architecture is fairly easy to understand. NIF's lasers operate in pulsed mode, the pulse energy coming from a massive capacitor bank. Just before the pulse is triggered, the capacitors discharge their energy into the laser amplifier crystals by way of flash lamps. A master oscillator starts the laser signal, which is split into 192 beams, amplified in the energized crystals, and frequency-tripled from red to blue. The whole amplification system is state-of-the-art, but even so, extremely inefficient – of the 422 MJ pumped into the capacitors, only 1.8 MJ makes it into the reactor chamber.
NIF uses an indirect drive approach to compress the pellet. In this appoach, the laser light is not shined directly onto the pellet, but onto a cylindrical capsule called a hohlraum about a centimeter in size. Within a matter of nanoseconds, the hohlraum reaches temperatures of 250–300 eV, immersing the fuel pellet in a uniform, superhot bath of X-rays, which compress the pellet and ignite a fusion reaction. The uniformity of this heat bath is the critical advantage of indirect drive, since this should prevent the onset of hydrodynamic instabilities like those that plagued NIF's predecessor, Nova. [5]
 |
| Fig. 4: Lasers vaporize the cylindrical hohlraum, which encloses a spherical deuterium-tritium pellet. (Courtesy of the Lawrence Livermore National Laboratory.) |
Laser systems operating in the megajoule range are predicted to undergo ignition with a gain of at least 10, and the NIF is expected to generate 20 MJ of fusion energy per pulse, although yields of up to 46 MJ are theoretically possible, [1,6,7]. Although ignition would be a milestone in its own right, the energy released at NIF would still be an order of magnitude less than the energy pumped into the capacitors to drive the laser, so the device does not even come close to breaking even from an engineering standpoint. In addition, NIF is only able to fire one shot every few hours, while a realistic reactor would need to fire around 10 times a second. However, by adapting technology from Livermore's Mercury laser, it appears very likely that these obstacles can be overcome. [8,9]
While NIF has been grabbing most of the media headlines, it is far from the only facility seeking to achieve ignition. A similar facility, the French Laser Mégajoule, is slated for completion in 2012. [5] A slightly different concept called fast ignition is being pursued by the Japanese at the FIREX facility, and the Europeans are planning a larger-scale fast ignition project of their own. [10,11] An entirely different method called the Z-pinch, which does not use a laser at all, it being investigated at Sandia Laboratories. [3,12] With so many competing designs and facilities, the next decade is sure to be an exciting one for inertial fusion research.
Of course, ignition is only worthwhile if the energy can be extracted efficiently. Recall that the DT fusion reaction produces a helium nucleus and a neutron:
There are two practical problems with this reaction. First, most of the energy is carried away by the neutrons, meaning that significant neutron shielding will be essential to any power plant. Second, while deuterium is commonplace, tritium does not exist in nature. It turns out that a solution to the first problem leads quite naturally to a solution to the second.
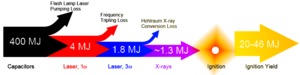 |
| Fig. 5: Energy budget in the NIF system and expected ignition yield. |
The neutrons are aborbed by a neutron blanket, a 60-cm thick "waterfall" of hot (900-1100 K) lithium that surrounds the reaction chamber and is perpetually cycled between the reactor (which heats it up) and a heat engine (which extracts the heat to produce electricity). This blanket absorbs 95% of the neutrons and all of the X-rays and fuel debris. Not only does this shield the neutrons and extract the energy from the reactor; it also breeds tritium through the following reactions:
This closes the fuel cycle by allowing us to generate, on-site, the rare but essential fuel element (T) from an element that is cheap and fairly abundant in the earth's crust (Li). The other fuel element, deuterium, occurs in large quantities naturally and can be extracted from seawater. [1]
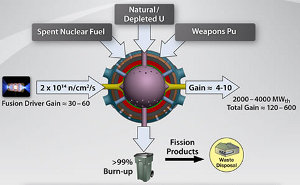 |
| Fig. 6: LIFE is once-through, "complete" burn-up closed fuel cycle. (Courtesy of the Lawrence Livermore National Laboratory.) |
Of course, these neutrons may be put to other uses as well. Consider that each neutron fission of a single uranium nucleus releases 200 MeV, about ten times more energy per neutron than the fusion reaction. This factor of ten forms the basis for the Laser Initiated Fusion-Fission Engine (LIFE), a reactor concept developed at Lawrence Livermore. A subcritical blanket of fissile fuel surrounds the reactor and absorbs its neutrons, further heating the blanket with fission products in the process. Because the fuel is always subcritical and fission is driven by fusion neutrons, not by a chain reaction, the LIFE reactor is inherently stable and cannot go critical. In addition, the constant neutron source allows LIFE to consume fuels that would otherwise be unsuitable in a standard nuclear reactor: depleted uranium, natural uranium, spent fuel (transuranic waste), thorium, and weapons-grade fuel can all be used. [13] LIFE engines could be extremely efficient – about 99% of all fissile fuels would be burned up in the LIFE cycle, and the amount of waste generated would be reduced by a factor of 20. [8] In this way, LIFE would function as the ultimate incinerator – you feed it nuclear waste, depleted fuel, and other unwanted products, and it gives you electricity, à la Mr. Fusion. [14]
Building a working fusion reactor would be a milestone in its own right, but when power executives gather around the marble table and talk about commercializing the concept, the billion-dollar-question is not "does it work" but rather "how much does it cost?" There is no way to answer this question, but a brief look at power plant efficiencies may provide some clues.
Regardless of the type of plant, the cost of electricity depends strongly on how efficiently the plant operates. The power produced by a fusion plant of any type will be given by an equation of the form: [6]
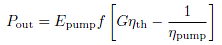
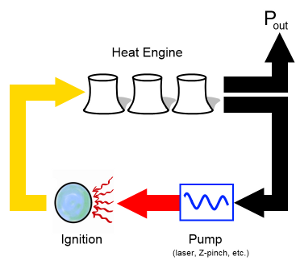 |
| Fig. 7: A fusion plant's power cycle. The energy generated from ignition must exceed the energy needed to trigger ignition. |
Here, Epump is the energy pumped into the DT pellet for each shot, f is the frequency of the system (the number of shots fired every second), and G is the gain, or the ratio of fusion energy to pump energy. The two efficiencies, ηth and ηpump refer to the heat engine and the pump. Typically, heat engines do not get much better than 40% efficient, so ηth ~ 0.3–0.4. The pump efficiency, however, can vary widely. For NIF's flash-lamp-driven lasers, it is ηpump = 0.66%, but diode technology borrowed from LLNL's Mercury laser could bump this up to 5%–13%. [9]
In order to make money, a power plant must at the very least produce more power than it consumes. In practice, one would like the output power to be significantly (at least a factor of 3) larger than the input power, from which we can derive a lower bound for the gain:
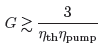
For NIF as presently constituted, this puts us at G > 1200, which will clearly not happen at NIF energies. However, switching from flash lamps to laser diodes increases ηpump by a factor of 10, giving us G > 65-170, a more reasonable gain. Recall that current NIF gain is capped at about G ~ 20. Fast ignition and LIFE technology both have the potential to multiply this factor by ten, easily pushing us over the threshold. This is the reason that scientists are pushing breakthrough technologies like diode lasers, fast ignition, and LIFE. Factors of 10 make a big difference in the gain calculus. And until we get the factors of ten right, there is little hope in obtaining an accurate price estimate.
Inertial Fusion Energy is a technology in its infancy, and it is possible that unforeseen scientific, technical, or economic reasons will prevent it from ever coming to fruition. But this is the peril of all basic research. Against these odds, though, stands the grand possibility of a clean, limitless, proliferation-free power source. Whether NIF will deliver on this promise, only time will tell.
© Ryan Hamerly. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] D. Keefe, "inertial Confinement Fusion," Ann. Rev. Nucl. Part. Sci. 32, 391 (1982).
[2] T. J. M. Boyd and J. J. Sanderson, The Physics of Plasmas (Cambridge, 2003).
[3] G. Yonas, "Fusion and the Z-Pinch". Sci. Am. 279, No. 2, 40 (1998).
[4] S. H. Glezner et al., "Symmetric Inertial Confinement Fusion Implosions at Ultra-High Laser Energies". Science 327, 1228 (2010).
[5] J. Jacquinot, "Fifty Years in Fusion and the Way Forward," Nucl. Fusion 50, 014001 (2010).
[6] J. Nuckolls, L. Wood, A. Thiessen & G. Zimmerman, "Laser Compression of Matter fo Super-High Densities: Thermonuclear (CTR) Applications," Nature 239, 139 (1972).
[7] J. Paisner, E. Campbell and W. Hogan, "The National Ignition Facility," Lawrence Livermore National Laboratory, UCRL-JC-117397, June 1994.
[8] E. I. Moses, "Ignition on the National Ignition Facility" a Path Towards inertial Fusion Energy," Nucl. Fusion 49, 104022 (2009).
[9] J. Caird et al., "Nd:Glass Laser Design for Laser ICF Fission Energy (LIFE)," Fusion Sci. Technol. 56, 607 (2009).
[10] H. Azechi et al., "The FIREX Program on the Way to Inertial Fusion Energy," J. Phys: Conf. Series 112, 012002 (2008).
[11] S. Atzeni et al., "Studies on Targets for Inertial Fusion Ignition Demonstration at the HiPER Facility," Nucl. Fusion 49, 055008 (2009).
[12] J. Chittendon, "The Z-Pinch Approach to Fusion," Physics World 13, No. 5, 39 (2000).
[13] J.C. Farmer, "LIFE Materials: Overview of Fuels and Structural Materials Issues" Lawrence Livermore National Laboratory, LLNL-TR-407386, October 2009.
[14] Back to the Future, Dir. R. Zemeckis. Universal Pictures: 1985, Film.