 |
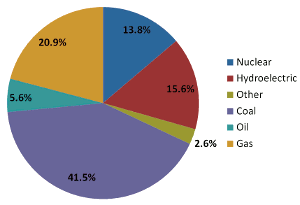
| Fig. 1: Total World Electricity Generation by Fuel in 2007 (Note: "Other" category includes solar, wind, geothermal and other renewables) [1] |
Burning coal is the most common method of generating electricity. It accounts for about 40% of world electricity generation. [1] By contrast, renewables (including hydroelectric, wind, solar, geothermal, etc.) cover less than 20%. This is not sustainable. Coal is a finite resource and eventually it will run out. This may be hundreds of years into the future, but it is important to consider this scenario before it becomes an imminent danger. The world electricity generation picture will necessarily look different as coal becomes more and more scarce.
It is hard to begin tackling the problem of coal running out when we think about this occurrence being a hundred or more years in the future. Fortunately, it is easy to determine how quickly we need to ramp up other sources of energy to be ready for that scenario using a simple growth model. By determining a required growth rate we can set yearly goals to make the problem much more manageable. Let us say that in n years coal will no longer be viable as a way to generate electricity. Assuming that consumption continues growing at rate r in the intervening time, the world will require power
| G = (C/E) (1+r)n | (1) |
where C is the current power consumption and E is the distribution efficiency. Something will have to cover the portion of electricity that would be generated by coal if it were still available. For this analysis we will assume that this is renewables. If j is the fraction of future power generation covered by renewables, then we have similarly
| jG = R (1+k)n | (2) |
where R is the current power generation from renewables and k is the growth rate of this power. Solving these equations simultaneously, we obtain for the required k
| k = (jC/ER)1/n ( 1 + r) - 1 | (3) |
Assuming the prototype values in Table 1, this gives G = 1.5 × 106 TWh/y and k = 0.037. This means that we could meet electricity demand in 150 years by increasing the rate of renewable use by 3.7% per year.
|
|||||||||||||||||||||||||||
| Table 1: Parameters used in Eqns. (1) - (3). Note that E assumes large future efficiency gains, and that the non-hydroelectric contribution to R in 2007 was only 474 TWh/y. C and R are the 2007 values. [1] | |||||||||||||||||||||||||||
The reader is encouraged to try adjusting the values of r, j, E, and n to model other scenarios.
At some point in the future, coal will no longer be able to be used to generate electricity. This is a serious problem, but we can develop a plan to replace coal by ramping up adoption of other forms of energy. By modeling future scenarios we can calculate the required rate of growth in renewable use in order to make the transition to a post-coal world as smooth as possible.
© Eric Glover. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] "Key World Energy Statistics", International Energy Agency, 2009.