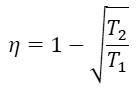
In classical thermodynamics heat engines are often analyzed without taking into account the irreversibilities which are always present in real engines. However, endoreversible thermodynamics makes some realistic assumptions about heat transfer and provides an upper bound for achievable thermal efficiencies under those assumptions. [1-3] These efficiency bounds tend to be tighter than the ideal Carnot bound and close to observed efficiency.
Curzon and Ahlborn showed that provided all the parts of an engine are ideal, but heat transfer is irreversible, the engine efficiency at maximum output power, also known as Chambadal-Novikov efficiency, is [3]
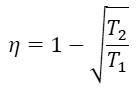
where T2 is the temperature of the heat sink, and T1 is the temperature of the heat source.
One of the assumptions they made was Newtonian heat conductance, i.e. the linear dependence of heat flux on the temperature difference between sink (source) and the working material. [3] If the input energy during the isothermal expansion stage is W1, it lasts for t1 seconds, the temperature of the working material is T1w, and α is a constant then
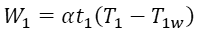
Similarly, for the isothermal compression stage with the output energy W2, duration t2, the temperature of the working material T2w, and the constant β we have
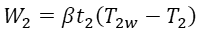
Reversible adiabatic stages are isentropic, so
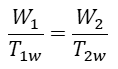
If the total cycle duration is proportional to isothermal stages duration with constant γ, the output power of the engine P is
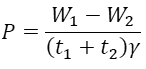
Assuming that x=T1-T1w and y=T2w-T2, the previous four equations together give
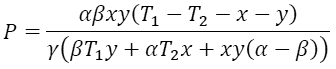
The output power P reaches its maximum when ∂P/∂x = ∂P/∂y = 0. These conditions lead to
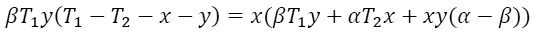
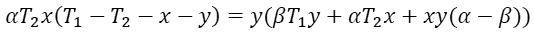
From these two equations we than have
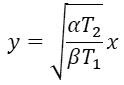
Substituting this expression into the earlier one, we
get a quadratic equation for x. Clearly, x
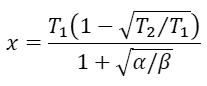
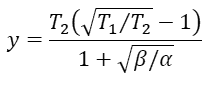
Finally, the efficiency at maximum output power is
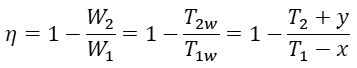
Remarkably, when x and y are substituted into the previous expression, α and β cancel out, and the final result is
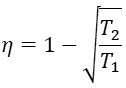
The following table compares Chambadal-Novikov efficiency with Carnot efficiency and with the observed efficiency for some real plants. As can be seen, the endoreversible efficiency is much closer to the observed data. It should be noted, that the above theory is not fundamental, it makes a few assumptions such as Newtonian heat conductance. As a result, if those assumptions are not completely valid, the observed efficiency can actually be slightly higher than the Chambadal-Novikov bound.
|
[1] I. I. Novikov, "The Efficiency of Atomic Power Stations," J. Nucl. Energy II 7, 125 (1958) [Atomnaya Energiya 3, 409 (1957)].
[2] P. Chambadal, Les Centrales Nucléaires (Armand Colin, 1957), p. 41.
[3] F.L. Curzon and B. Ahlborn, "Efficiency of a Carnot Engine at Maximum Power Output," Am. J. Phys. 43, 22 (1975).