|
|
| Fig. 1: Rotating drum with superfluid in it. When fluid (blue) is encircling the wire and the wire is vibrating, the magnus force induces circular motion in the wire, as indicated by the pink arrow. The circulating fluid is dragged along with the wire. |
A superfluid is a state of matter that, like an ordinary fluid, can flow and take the shape of its container. When you excite a normal fluid by putting a stationary object in flowing water, vortices will develop or the flow will become choppy. [1] This turbulent behavior is absent when exciting superfluids in a similar manner and it takes more than just an object impeding flow for the superfluid to develop excitations. An interesting class of experiments is to controllably vary the disturbing force applied to the superfluid and see at what level the flow of the superfluid changes. One such way is to see how the motion of the superfluid responds when it is a rotated at various rates.
Circulation is a number that quantifies how quickly a fluid moves around a closed path. The expression for circulation in ordinary liquids is the product of the average velocity of the fluid along the path multiplied by the length of the path, so faster flows of the fluid yield a larger value. As an example, consider the circulation of a fluid at the walls of a rotating bucket. By controlling the rate of the bucket's rotation you can get the circulation of the fluid at the walls to match that of the bucket.
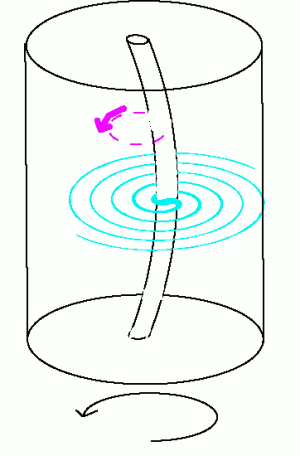
Discovered in 1937, Superfluid Helium forms spontaneously when Helium is cooled below 2.17 K (-456 F). In 1960, W.F. Vinen invented a clever technique to measure the circulation of superfluid Helium around a thin wire. [2] The superfluid was placed inside a 4 mm diameter drum of length 5cm and was set rotating by spinning the drum as shown in Fig. 1. By 1979 W. Zimmerman, Jr. improved Vinen's ideas and obtained the data for circulation as a function of rotation rate shown in Fig. 2. [3,4] Whereas a regular fluid's circulation should increase continuously with the rotation rate, a superfluid changes in discrete steps. This is a clear indication of the non-classical nature of the superfluid. The measurement relies on a phenomenon known as the Magnus Effect. [5,6] If a fluid is circulating around a wire and the wire is then dragged in the x direction, the circulating fluid will pull the wire in the perpendicular y direction. This is shown in Fig. 3. The greater the circulation, the greater the force with which the wire is pulled.
 |
| Fig. 2: Circulation of liquid Helium about a wire as a function of the rotation rate of the drum. The drum's rotation rate was swept in the direction of the arrow the graph strongly shows the quantization steps in the circulation, which is clear evidence of non-classical behavior. There is also hysteresis in the sweep. |
 |
| Fig. 3: The magnus force is the perpendicular lift force on the wire when it and the vortex are dragged at velocity V. |
The wire, like a string on a musical instrument, has a specific frequency at which it vibrates when you pluck it. In fact, the wire can vibrate in two different ways and produce the same frequency: it can vibrate in the x-direction or the y-direction. These are the two fundamental modes of the wire and they are called degenerate. Now, consider Vinen's wire in the presence of circulation: if you excite the wire in the x-direction, the Magnus Effect simultaneously excites the wire in the y-direction. The vibrations in the x and y directions are no longer the fundamental modes of the system because they can't exist independently. Instead, plucking the wire will excite two circularly rotating vibrations, and it is these that are the new fundamental modes. One of these modes is shown in Fig. 1.
The coupling of the degenerate x and y modes through some sort of interaction is a well known problem in physics. The important result is that the new rotational modes are no longer degenerate—they spin in a circle at different frequencies. The presence of frequency splitting of the modes is therefore an indicator that circulation is present in the system. You can calculate an explicit relationship between the two quantities, so by measuring the splitting you are measuring the circulation.
If you hold a magnet up to a light bulb, you will notice that the filament will vibrate. This is because a magnetic field will exert a force on the current and pull the wire sideways. By sending a short pulse of current through his wire in the presence of a magnetic field, Vinen momentarily deflected the wire off-axis in the x-direction and then the natural springiness of the wire pulled the wire back, starting the vibration. There is a dual effect that the motion of a wire in a magnetic field will induce a current in the wire, provided that the wire is a part of a closed circuit. After Vinen's wire was displaced by the initial current pulse, subsequent vibrations of the wire induced a current, which was then measured. Since the wire's motion consisted of oscillations at two frequencies, a corresponding electrical signal was induced in the wire. The problem of measuring the difference in the two vibration frequencies, and therefore circulation, was transformed into problem of measuring the same thing on an electrical signal.
Musicians are familiar with the concept of the beat note, which occurs when two notes of different frequencies are played simultaneously. The beat note is a modulation of the intensity of the sound wave and has a frequency equal to half the difference between the two constituent frequencies. The current induced in the wire has the same beat effect as illustrated in Fig. 4. The difference in frequency between the two modes is inversely related to the duration of a single beat, τ, which can be easily measured by plotting the signal on an oscilloscope. The circulation can then be calculated from this quantity.
 |
| Fig. 4: Diagram of a scope trace illustrating the beat pattern of the two frequencies following an initial current pulse. Zimmerman measured t, the time different between the first and second beat nodes, to obtain the beat frequency. Vinen measured the time of the first beat node. |
 |
| Fig. 5: Quantum waves encircling the wire. The first waveform has 8 wavelengths and corresponds to a circulation of 8 h/m and the second waveform corresponds to a circulation of 3 h/m. |
In addition to these procedures, there were many complicated factors that needed to be addressed which would have interfered with an accurate measurement. The two fundamental modes of the wire may have already been split due to various internal stresses and strains in the wire. Imperfections in the electronics appended noise spurious signals to the current going through the wire. The direction of magnetic field needed to be aligned correctly with wire to properly induce the wanted signals. Variations in the wire’s linear mass density needed to be carefully considered. Nontrivial metastable excitations of the superfluid may have spontaneously attached and detached from the wire, changing the measured circulation. Vinen's measurements consequently had some ambiguities and he was unable to obtain good circulation data as a function of rotation rate. Instead, he examined how the circulation depended on a function of time after the rotation of the drum containing the superfluid was suddenly stopped. He was able to collect evidence to show that the circulation preferentially relaxed to two stable: 0 and .1 mm2/s. The latter number is equal to h/m where h is Planck's ubiquitous constant that appears when quantum effects are relevant and m is the mass of Helium.
Zimmerman's results, shown in Fig. 2, are much more conclusive. Starting with the drum at rest, he slowly increased the rotation rate to 3.7 radians per second and then slowly decelerates the drum until it is rotating at 3.7 radians per second in the opposite direction. He then accelerates back to zero with each cycle took between 8-10 hours. The data unambiguously shows that the circulation is quantized - it can only take on values that are integer multiples of a fixed constant. Zimmerman repeated the experiment for four wires and measured that for each wire this constant is, in units of h/m, 0.981(0.003), 0.839(0.004), 1.009(0.005) and 0.988(0.004), respectively. While the constants vary from wire to wire, they are the same for separate runs of the same wire, and all values are close to h/m. This strongly implies that quantization of circulation is a fundamental aspect of superfluids. That the values are not exactly equal to one suggests that there was either further physics at work, or that there were unaccounted sources of error in the measurement.
In 1949 Lars Onsager first predicted that circulation is quantized in superfluids. [1] Onsager hypothesized that the values of the quantized circulation are given by the formula k=Nh/m, where N is an integer. This formula is an ansatz - an intuitive guess, not derivable from any more fundamental theory. That Vinen's and Zimmerman's experiments strongly support this hypothesis is remarkable, especially considering that a general theory of superfluid Helium continues to elude scientists today.
One of the principles of quantum mechanics is that matter can behave both like a particle and a wave. We imagine particles as point-like objects that can bounce off each other like two billiard balls might. Waves on the other hand can add and subtract to each other in the same way two surface waves on the ocean will superpose and pass through each other. The theory of quantum mechanics successfully reconciles these two seemingly contradictory views of matter into a coherent and well-tested picture.
If a single atom can be thought of as both a particle and a wave, then one might suspect that an ensemble of atoms also has properties of an ensemble of point-particles, as well as some of a single wave. [7,8] The quantity that would be "waving" is not the density of the fluid, as in a sound wave, nor a wave in the height of the fluid, as in a surface wave on the ocean. It is some other quantity, often called the phase or the order parameter. The concept of phase is a well tested aspect in the quantum theories of single particles, so it is natural to consider this idea with superfluids.
In quantum mechanics, the velocity of a particle is inversely proportional to the wavelength of the wave. The same relationship can be applied to the circulation of a superfluid about a wire. A wave can travel around a wire only if, after one revolution, the wave looks the same as it did when it started; otherwise it would cancel itself out after many revolutions. Therefore, the only waves that can encircle a wire are those that have an integer number of wavelengths in one revolution of the wire as in Fig. 5. In this picture, the number of wavelengths that can fit around Vinen's wire is proportional to the measured circulation, and this offers an explanation for why the jumps in circulation are roughly the same in Fig. 2.
© 2009 Alexander Fried. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] "Fluid Mechanics - turbulence - cool science" Youtube Video http://www.youtube.com/watch?v=vQHXIHpvcvU&feature=related
[2] W. F. Vinen, "The Detection of Single Quanta of Circulation in Liquid Helium II," Proc. Roy. Soc. A 260, 218 (1964).
[3] S. C. Whitmore, "Observation of Quantized Circulation in Superfluid Helium," Phys. Rev. 166, 181 (1968).
[4] P. W. Karn, "Observation of Quantization of Circulation in Rotating Superfluid Hellium," Phys. Rev. B. 21, 1797 (1980).
[5] D. J. Thouless, "Transverse Force on a Quantized Vortex in a Superfluid," Phys. Rev. Lett. 76, 3758 (1996).
[6] H Lamb, Hydrodynamics (Dover, 1945).
[7] A. Corrada-Emmanuel, "Algebraic Topology and the Quantization of Circulation in Superfluid Helium," Phys. Rev. B 45, 2553 (1992).
[8] R. J. Donnelly, Quantized Vortices in Helium II (Cambridge, 1991).