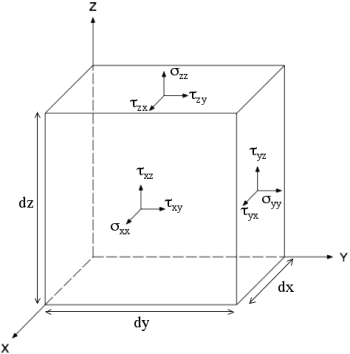
 |
| Fig. 1: The nine force components of the stress tensor on an infinitessimal fluid element. |
Lubrication is the effect of a viscous fluid positioned between moving surfaces. It plays an essential role in mechanical systems, both man-made and in nature, because it prevents the wear that results from repetitive surface friction. In general, lubricated systems contain a mixture of surface friction and lubricant friction, and are difficult to model. However, during hydrodynamic lubraction the lubricant is sufficiently thick that the surfaces do not make contact, and the laws of fluid mechanics along with boundary conditions given by adhesion govern most of the physical properties of the system. I will focus on this simplified form of lubrication, as it is the first step to understand more general situations. I will begin by a brief review of the basic hydrodynamic equations, apply them to a simple geometry called the journal bearing, and finally discuss some important properties of actual lubricants.
Consider an infinitessimal element of a viscous fluid with a stress tensor that gives the normal and sheer forces on each face (Fig. 1):
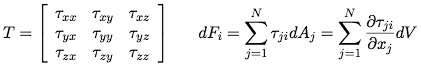
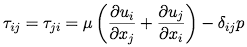
In order to include the effect of a viscocity of compression that resists changes in the volume of the fluid, we add an extra term to the diagonal elements that is proportional to the divergence of the velocity field by a constant λ.
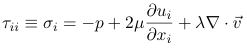
The viscocity of compression, μD, is then defined such that when it vanishes, the trace of the stress tensor is just equal to the pressure acting on each of the three sides (that is, the fluid element itself offers no additional resistance).
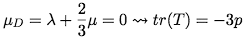
So for a newtonian fluid, in which the viscocity is independent of the shear, the stress tensor is given by
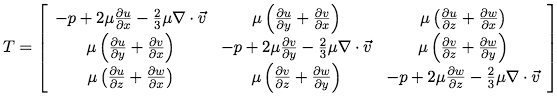
Finally, the dynamics of the fluid are determined by an anologue of momentum conservation called the Navier-Stokes equation (NSE) and a mass continuity equation, where ρ is the fluid density, D/Dt is the substantive derivative, [u v w] is the velocity field of the fluid, and [X Y Z] describes an external force.
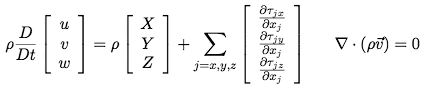
We now consider the journal bearing, the most fundamental surface geometry. This arises when a cyclindrical shaft is made to rotate inside of a bearing with an oil or grease lubricant in the gap. When the shaft spins with large enough rotational velocity, it becomes well coated with lubricant and the surfaces cease to make contact. The symmetry in this setup allows us to consider only a 2-dimensional cross section of the gap bearing gap (Fig. 2) so gain an understanding of the entire system.
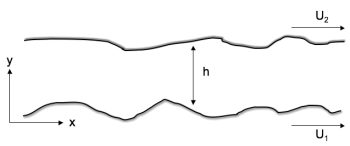 |
| Fig. 2: The Journal Bearing. Two surfaces with viscous lubricant between them thick enough that they do not make contact move with different speeds. |
To further simplify things, we will assume perfect adhesion, such that at the surfaces the velocity of the fluid matches the velocity of the walls. This gives two boundary bonditions, and we expect that the velocity profile of the fluid varies continuously from the one wall to the other. To get the exact form of this variation we must consider the NSE. The case where the surfaces have infinite extent in both horizontal directions was tackled by Reynolds, and I will now trace through his derivation.
Reynolds made several more simplifying assumptions: all the flow is laminar (there is no turbulence), there are no external forces, intertial forces are small compared with shearing (D/Dt(u,v,w)≈0), and that du/dy and dw/dy are much larger than all other velocity derivatives beacuse the y-dimension is small. Plugging all these assumptions leaves a simplified NSE [1]:
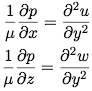
For perfect adhesion, the boundary conditions are once again
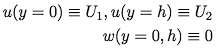
We can integrate twice using these boundary conditions to get expressions for the u and w velocity components of the fluid.
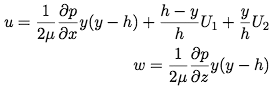
If we plug these velocities into the mass continuity equation,
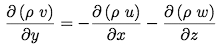
and integrate over y subject to v(Y=0) = V, we eventually arrive at the Reynolds equation.
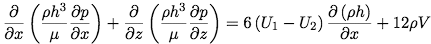
This equation determines the pressure profile of the fluid as a function of the the h(x) surface geometry and the relative velocity of the walls, and can be modified to accurately describe almost any bearing. The left hand side represents the shape of the pressure distribution, while the first term on the right represents the effect of fluid being driven by thicker parts of the surface gap to thiner parts by movement of the walls and the second term represents squeezing of the fluid in the normal direction due to the variation in the surface gap [4]. While the Reynolds Equation is an inhomogeneous PDE and not generally easy to solve, the densities cancel if we assume that the fluid is incompressible (a good approximation for oil lubricants). After this, some h(x) geometries do admit analytical solutions [1]. In the case where the length of the bearing is finite however, the equations must be solved numerically [4].
The journal bearing was a simple enough example to be analytically solvable, but any surface geometry with a viscous fluid and adhesion will result in the property of lubricants to prevent mechanical wear by taking up the frictional forces. Tribology is the (often empirical) study of friction and wear and looks at some design features in a good lubricant. I'll introduce empirical forms for the viscocity and density used in the hydrodynamic equations, and particulate contamination, an area of importance in design of real systems
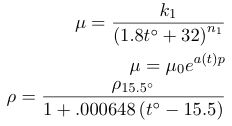 |
| Box 1: Commonly employed empirical forms for the pressure and temperature dependences of viscocity and density of oils where constants k1, n1, μ0 ρ15.5°, and the function a(t) are determined by the lubricant, and all temperatures are given in degrees centigrade [2]. |
In all the above derivations, we assumed that the fluids were Newtonian, meaning that frictional force per unit area in the fluid depends linearly on the velocity gradient. This lead to a constant of proportionality we called the viscocity. However in general this relationship is just a nonlinear power series, leading to a viscocity that is a function of the velocity gradient [2]. Further, the viscocity and the density of the lubricant are also functions of the pressure of the fluid and concomitantly its temperature. Various empirical forms of these relationships exist, but are not derived from first principles (see Box 1). These relationships complicate the equilibrium solutions of the Reynolds equation because the variation of the friction in bearing gaps generates a heat profile in addition to a pressure profile, and this in turn generates a variation in the viscocity across the gap [2].
As just mentioned, friction in the fluid generates heat, and so true thermohydrodynamic lubrication is the theory that is satisfies both the Navier-Stokes Equation and the heat equation, including a balance of heat transfer into the walls of the lubricant and heat generation inside the lubrication. Such an approach is useful in part because the amount of heat generation is essentially the loss of mechanical energy of the bearing, so there is a need to be able to accurately estimate it.
There are numerous other subtle factors impacting a realistic model of lubrication, many involving the the fact that the walls are not perfectly hard and solid. For instance, if the walls may bend under strain, then local shearing by the lubricant introduces an additional term to the right side of the Reynolds Equation proportional to the variation in horizontal velocity of the walls with x. There may also be general deformations of the entire bearing depending on the magnitude of the load [2].
If the walls are not perfectly hard, solid particles may occasionally break off just from shearing of the surface by the lubricant. These contaminants may become lodged in the bearing gap if their maximal dimension is larger than the minimal horizonal size of the gap, resulting in further accelerated wear [5]. If the contaminants are smaller, then they will simply act as an abrasive which occasionally striking the walls, also resulting in wear.
© 2007 Michael Jeremy Rosen. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] O. Pinkus and B. Sternlicht, Theory of Hydrodynamic Lubrication (McGraw-Hill, 1961).
[2] N. Tipei, Theory of Lubrication (Stanford University Press, 1962).
[3] N. Suh, Tribophysics (Prentice-Hall, 1986).
[4] Y. Hori, Hydrodynamic Lubrication (Springer, 2006).
[5] Y. A. Williams and A. M. Hyncica, "Abrasive Wear in Lubricated Contacts," J. Phys. D 25, A81 (1992).