One of the most exciting developments in astronomy over the past decade has been the discovery of a large number of extrasolar planets in nearby star systems; discoveries that have finally begun to shed real, experimental light on the possibility of planets and life beyond our own solar system. We will elucidate one narrow range of this topic by first discussing the fundamental orbital mechanics that enable us to detect extrasolar planets. Next, we consider the puzzling question of why so many of the extrasolar planets detected thus far have highly eccentric orbits, unlike planets in our solar system. Eccentricity can have a profound effect on the geological behavior of planets, in addition to their prospects for supporting life. One possible model to describe the observed distribution of eccentricities, the Kozai mechanism, is subsequently introduced and discussed.
Direct observation of extrasolar planets has, to date, proven to be difficult if not impossible. The reasons for this are fairly straightforward: the brightness of the central star is usually several orders of magnitude larger than that of the planet(s) and thus the planets are difficult to resolve. While future space telescopes will attempt to directly observe extrasolar planets in the infrared region, the most productive detection method that has been used to produce the past decade's many discoveries is an indirect one: Doppler spectroscopy.
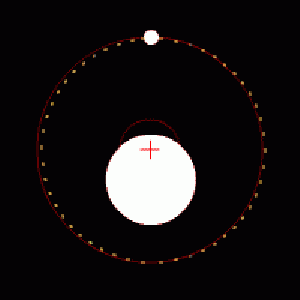
The basic idea is, in itself, quite simple. Any planet orbiting a star causes the star itself to "wobble" as they orbit around their mutual centre of mass (see Figure 1). This wobble would cause the star's radial velocity to shift in a periodic manner; this was predicted decades ago to cause small, periodic Doppler shifts in the star's emitted radiation. To translate the amplitude of the variation in spectral lines (the Doppler shift) into an actual meaningful estimate of the extrasolar planet's we must consider some basic orbital mechanics. From Kepler's third law we have that:
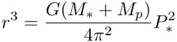
Since
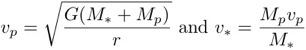
and K = v*sin(i), where K is the half-amplitude of the observed oscillation, and i is the inclination of the planet's orbit to our line of sight, we can derive the standard expression for K which in turn allows us to derive planetary parameters once K is known. Note below that we also account for the eccentricity of the orbit:
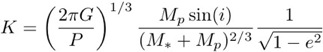
Depending on the sensitivity of one's telescopes and spectrometers one can detect fairly small reflex velocities (ie: the amplitude K). To put this into tangible terms we plot a graph of mass M_p in units of M_Jp (Jupiter masses) vs. radius (the semi-major acis of the orbit) in AU. The relationship between the two is derived from the above expression, substituting in for P by Kepler's Law:
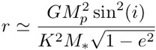
The constant lines in Figure 2 represent specific reflex velocities and hence potential limits of detectability. For reference Jupiter, Saturn and the Earth are plotted on the graph. With this, it is easy to see why the first extrasolar planets detected were large (Jupiter or larger) sized planets that orbited relatively close to their star. As sensitivities and signal-to-noise ratios have improved, and in conjunction with techniques like photometry, astronomers have been able to detect smaller rocky planets like the Earth.
We can also clearly discern the challenges and limits of this indirect approach to detection with this graph. To detect a planet similar to earth (similar size and distance) would necessitate being able to detect spectral shifts on the order of 0.01m/s. This tangible translation of real orbital parameters to experimental sensitivity requirements is the first main point in this report. Namely, a large planet orbiting close to a star is easier to detect with doppler spectroscopy. However, such planets are much less likely to be life-supporting.
To date, some 150 extrasolar planets have been discovered by the radial-velocity method just described. Of these, 20% are orbiting a binary star system. As was noted earlier, one of the most puzzling results of these detections has been their high orbital eccentricity. The median eccentricity observed is 0.28, which is much higher than the highest eccentricity observed in our solar system (that of Pluto). Researchers have argued that these eccentricities are not seriously affected by observational selection effects [1] and thus represent an actual physical trend.
The general theory of planetary formation posits that planetary systems are formed for circumstellar disks. One would generally expect such symmetric disks around a source star to yield planets with circular orbits. If we then assume that these planets started out with circular orbits then we can investigate mechanisms that would perturb the orbits and increase their eccentricity. The mechanism we introduce here is that discussed by [1], a secular interaction with a distant companion. This is motivated by the fact that 20% of extrasolar planets discovered so far are in so-called wide-binary star systems - where the central star is orbited by a companion at some non-small distance.
The Kozai Mechanism is a secular interaction between a wide-binary companion and a planet in a triple system. In particular when the relative inclination angle between the two orbital planes is greater than 39.2 degrees (known as the Kozai angle) a cyclic and long-term exchange of angular momentum occurs between the planet and more distant companion. This results in a long-period oscillation of both the eccentricity and the inclination where the following value is conserved for eccentricity e and inclination i (relative to the orbit of the perturbing body) [3]:
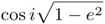
Thus, almost circular but highly inclined orbits could become very eccentric over time with their inclinations becoming smaller correspondingly. This then provides one possible means of inducing highly eccentric orbits in initially circular systems. Some other key features of Kozai oscillations include:

It now becomes useful to describe the nature of the binary companions that we've only generally described. Astronomically, there are two main/prevalent types of binary companions: Brown Dwarfs and Main-Sequence Dwarf stars. The main difference between these two types (for our purposes) are with respect to their masses. Brown dwarfs are much smaller than a star (MSun) in mass, and can have larger orbital ranges (their masses can approach Jupiter masses), while main-sequence Dwarf stars are about the same mass as the sun. With this detail discussed, we now consider the period of the Kozai eccentricity oscillation; a period which can be estimated as [3]:
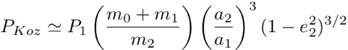
Here, the 0 index refers to the central star, 1 refers to the planet and 2 refers to the binary companion. The Kozai period described above is relevant, as it tells us how often a given planet in a particular system could find itself in a high eccentricity orbit. If the Kozai period is as large as the lifetime of the star or system, then it is unlikely it is highly eccentric at a given point in time. The period is inversely proportional to the mass of the binary companion. So, brown dwarfs, with masses ~ 0.01MSun would have oscillations 100 times longer than that of a main-sequence dwarf star!
In Figure 3, we outline the range of the Kozai Mechanism in terms of the mass and period of the binary companion. To accomplish this we rewrite the above expression using Kepler's Third Law and rearrange as follows:
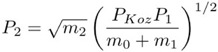
Specifically, we see that the Kozai mechanism can either be too slow and the planet would not have enough time to complete one full cycle within the lifetime of the system, or the relativistic precession period of the system is shorter than the Kozai period, thereby supressing and dominating those oscillations. Thus, the smaller the mass of the companion, the shorter its period needs to be for a Kozai oscillation to be possible and relevant. To actually compute the eccentricity variation/oscillation over time necessitates numerically integrating a fairly complex system of octuple-order secular perturbation equations (a system of three nonlinear differential equations). We refer the reader to [3] for a thorough derivation and solution to this problem. For our purposes we note that two dwarfs have the same parameters except that the brown dwarf's mass is 10x smaller than that of the main-sequence dwarf, would imply that the brown dwarf's Kozai period is 10x longer than that of the main-sequence dwarf.
In summary, we have introduced the concept of doppler spectroscopy and subsequently delved into a key puzzle noticed by astronomers - the high orbital eccentricity of extrasolar planets. We then considered the Kozai mechanism, a secular perturbation that allows for oscillations in eccentricities and inclinations, as a source of these high observed eccentricities. Clearly, such mechanisms can only occur in some form of binary-companion system, which comprise a significant percentage of the systems where extrasolar planets have thus far been detected. The referenced literature further considers several models of eccentricity distribution against the observed distribution. They finally argue that even though this is constrained to binary systems, the results show that Kozai-like perturbations from other bodies in a system could be responsible for shaping the eccentricity distribution across all star systems. Ultimately, this is just one possible model/mechanism to explain the observed phenomena. Indeed, it is as yet unclear whether a large percentage of extrasolar planets exist around binary systems or if this is a function of local and/or selection bias. Thus far, we have been searching for planets in our neighborhood, which may have certains quirks and biases relative to the rest of the galaxy.
However, the very fact that we can discuss these scenarios is made possible by our recent ability to truly take advantage of lower limits in doppler spectroscopy. The coming decades should prove to be even more exciting and illuminating as new space telescopes and better photometric techniques improve our knowledge of the nature of planets outside our solar system.
© 2007 Aaswath P. Raman. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] G. Takeda and F. A. Rasio, "High Orbital Eccentricities of Extrasolar Planets Induced by the Kozai Mechanism" Astrophys. J. 627, 1001 (2005).
[2] G. W. Marcy and R. P. Butler, "Detection of Extrasolar Giant Planets," Ann. Rev. Astron. Astrophys. 36, 57 (1998).
[3] E. B. Ford, B. Kozinsky and F. A. Rasio,"Secular Evolution of Hierarchical Triple Star Systems," Astrophys. J. 535, 385 (2000).