The curveball is now a central component in the game of baseball. Thrown by imparting spin onto the baseball during release, the force arising from the interaction of the baseball's spin with the surrounding air often causes deflections of more than a foot from a free-fall trajectory. This paper reviews the experimental and analytical work done on understanding the physics behind what makes the curveball curve.
Invention of the curveball is credited to William "Candy" Cummings [1]. In 1863, Cummings discovered that he could cause a baseball to curve downward by rolling the ball off his second fingertip and accompanying his usual throwing motion with a hard torque of the wrist to impart topspin on the baseball. Cummings spent the next several years improving his control over the new pitch, and, according to baseball lore, used it for the first time in a game in which his club, the Brooklyn Excelsiors, defeated Harvard College in 1867. Cummings went on to have a successful baseball playing career, including playing during the inaugural season of the National League in 1876, and is enshrined in Baseball's Hall of Fame.
However, long before people knew how to throw curveballs, it was recognized that the spin of a spherical projectile can substantially alter its trajectory. In fact, Newton recognized that the fact that tennis balls curve is due to spin imparted upon them in 1671 [2]. In 1877, Lord Rayleigh, also discussing curving tennis balls, credited the German engineer G. Magnus with the first explanation of the lateral deflection of a spinning ball, and as a result the effect is generally called the Magnus effect [3]. Historians of science now understand that Magnus' explanation had its origins in 1742 in a book by a British scientist B. Robins in his book New Principles of Gunnery in which he analyzed the effects of spin on flying cannonballs and musket balls.
The elements of the Magnus' and Robins' explanation are quite simple. A spinning ball causes a whirlpool of air around it. Air flying past the ball will flow more quickly on the side of the ball in which the flow velocity is parallel to the spin velocity of the ball, and will flow more slowly on the side in which it opposes the spin. Bernoulli's principle states that the sum of the kinetic energy and the pressure of a fluid is constant, so that there will be an increase (decrease) in pressure on the side of the ball in which the spin opposes (reinforces) the airflow. This pressure imbalance causes a net overall force perpendicular to the ball's velocity. In the case of a spinning baseball with topspin, the pressure is higher above the ball than below it, causing a net downward force on the ball.
 |
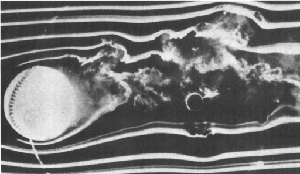
| Fig. 1: Airflow near a spinning baseball. Ball is spinning counterclockwise at 30 rev/s and the wind speed is 47 mph to the right [4]. |
The essential physics involved with this explanation can be visualized in Figure 1, which consists of a photograph of a spinning baseball in the presence of smoke. The smoke streams are released with equal spacing at their source to the left of the ball, and the counterclockwise spin of the ball causes the smoke streamlines to bunch at the bottom edge of the ball. This closer spacing is indicative of increased air velocity, which as discussed above, indicates a pressure deficit and a downward force on the ball. A downward force can also be explained by noting that the smoke wake is deflected upwards, which by Newton's Third Law must correspond to an equal-but-opposite downward force on the ball.
Before discussing the experimental work on baseball trajectories, it is useful to consider the general properties of the motion of an object through a fluid. The fluid can impart two general types of forces on a moving body, which are defined relative to the translational velocity u of center of mass of the baseball. Firstly, the drag force D opposes u and is a frictional force proportional to u. The force we shall generally be concerned with is the lift force FL, which acts perpendicularly to both u and the ball's spin vector &Omega. The general theory of the aerodynamics of a moving body dictates that the lift force is given by
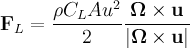
where &rho is the mass density of the air, A is the cross-sectional area of the ball, and the lift coefficient CL, a dimensionless constant, will be a function of several parameters:
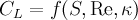
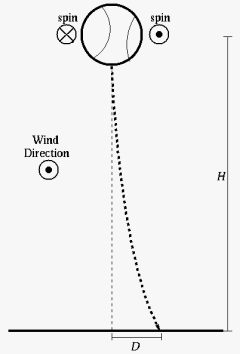 |
| Fig. 2: Diagram of Briggs' experimental setup for tests of lateral deflection of baseballs in a wind tunnel. |
where S, Re, and &kappa are dimensionless variables. S is the spin parameter of the ball, and relates the speed of a point on the ball's equator to the translational speed and is given by &Omegar/u. Re is the Reynolds number, a parameter which relates the inertial forces to the viscous forces acting on the baseball, and is given by 2ur/&nu, where &nu is the kinematic viscosity of air. Because &nu can change depending on environmental conditions, weather and altitude can affect the ball dynamics through a dependence of CL on Re. The final factor &kappa describes the ball's roughness, and is given by &Deltar/r, where &Deltar is a measure of the maximum excursion of the surface from a true sphere. &kappa conceivably could depend on the orientation of the seams of the baseball relative to the spin axis, and also can be used to compare sports balls of various types (golf balls, soccer balls, etc). Several experiments on the aerodynamics of spinning balls report a near-linear dependence of CL on S, only a very weak dependence on Re, and critical behavior in which CL switches sign as &kappa approaches 0. These experiments are discussed in the following sections.
L. Briggs, in 1959, did the first systematic study of baseball deflection as a function of u and &Omega published in mainstream scientific literature [5]. His experiments, a schematic of which are shown in Figure 2, were done by dropping a spinning baseball into a wind tunnel. Briggs spun the baseball using an electric motor in which a rotating shaft was attached vertically to the ball by a valve-controlled suction cup such that the spin axis was parallel to gravity. The ball, coated in a colored lubricant, was dropped into the wind stream and the deflection from vertical was recorded twice, once with the ball spinning each direction relative to the wind. The average deflection D was measured for several u and &Omega.
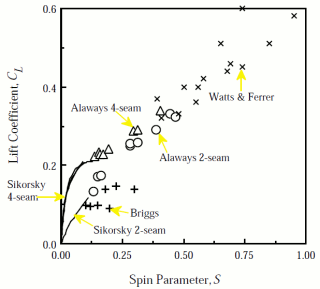 |
| Fig. 3: Conglomeration of experimental results on curveballs [11]. (Reproduced by permission of LeRoy Alaways.) |
Briggs' data has been shown to be consistent with later experiments, but he came to some erroneous conclusions. Firstly, Briggs' extrapolation that a nonspinning ball (&Omega = 0) experiences no deflection has been shown to be inconsistent with an experiment by Watts and Sawyer in which strong (FL/mg ~ 0.3) orientation-dependent lift forces were observed [6]. In addition, Briggs observed that D varied with the square of u, a result that agreed with C. Drury's reports of experiments done by Sikorsky [7]. This result, however, does not agree with the Kutta-Zhukovsky theorem from aerodynamics, which states that a net circulation of an inviscid fluid about a two-dimensional object results in a force proportional to the product of the velocity and the circulation [8]. Therefore, it is reasonable to expect that the lift force would be proportional to &Omegau, as had been seen in a study on golf balls [9], rather than &Omegau2, as Briggs suggests.
In 1986, Watts and Ferrer extended Briggs' methods to explore this controversy, and presented the first discussion of baseball dynamics phrased in terms of the three dimensionless parameters above [watts]. Watts also used Briggs' wind tunnel technique, and performed experiments for the largest S values in the scientific literature, out to S &asymp 1.0. Another very systematic study was completed by Alaways in 1998, using a more modern technique of high speed video capture of pitches thrown by both humans an pitching machines. He used a parameter estimation by fitting to an analytical model of baseball trajectories including lift and drag forces, and plots these trajectories along with those where the pitches in comparison to those without aerodynamic forces (free-fall) [11].
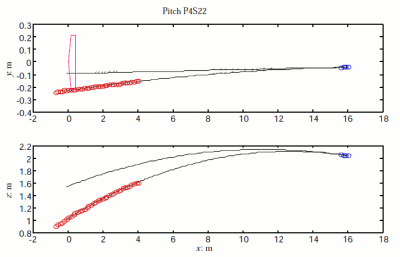 |
| Fig. 4:Trajectory of a machine-thrown curveball with initial velocity of 77 mph with a spin of 24 rev/s [11]. (Reproduced by permission of LeRoy Alaways.) |
Figure 3 shows a conglomeration of experimental results including the work discussed by Briggs, Sikorsky, Watts and Ferrer, and Alaways. Note that the 2-seam or 4-seam orientations correspond to the number of seams intersecting the equatorial plane of the spinning baseball. Figure 4 shows an example trajectory of a pitched curveball and compares it to the arc taken by a ball with the same initial velocity but without spin. It is worth noting that
Other data of Alaways shows that CL is approximately independent of Re for all ball velocities studied. Briggs' data and the Watts/Ferrer data also confirm this.
Work on the aerodynamics of smooth spheres shows an anomalous Magnus effect of opposite sign. This counterintuitive effect was also investigated experimentally by Briggs, but was not studied analytically until 2003 [12]. Borg et al. studied the forces on a spinning sphere in the limit of rarefied gases. In this limit of low density, and correspondingly low viscous forces and large Re, the gas is treated as a set of ballistic particles, and the theory is only valid in the regime in which the mean free path of gas particles is larger than the size of the sphere. They find a negative lift coefficient proportional only to the product &Omegar. In order for CL to be independent of u, it must be linearly dependent on both Re and S, which is exactly what Briggs' data showed.
Just as there is an intuitive explanation of the Magnus effect in terms of Bernoulli's principle, Borg gives an explanation of this inverse Magnus effect in terms of momentum conservation. Gas particles preferentially hit the windward face of the sphere, and are primarily deflected along the motion of the spinning surface. In the case of a ball traveling forward with topspin, this indicates a deflection of gas particles downwards, which must correspond to a net upward force on the sphere, opposite to the Magnus force which tends to push a curveball downward.
Because of the complexity of the surface of the baseball and the mechanism of boundary layer separation for turbulent flow, it is impossible to analytically solve the functional form of the dependence of CL on S, Re, and κ. Experimental work completed since the 1950s shows that
Most baseball players report that a curveball is often seen to "break," or suddenly alter its trajectory. This effect can only be an optical illusion, as studies of baseball trajectories indicate that the Magnus force acts downward during the entire flight of the ball, giving it a parabolic trajectory [11]. From a batter's perspective, however, the majority of the deviation from a straight line occurs in the last moments as the ball approaches home plate.
There have been extensive studies of other sports balls in which the effects of spin on lateral deflection are studied. The same effects that force a ball with topspin downwards also act to keep a golf ball with backspin in the air for longer than a non-spinning ball. An excellent review of sports ball aerodynamics has been given by Mehta [4].
© 2007 Jason Pelc. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] D. Fleitz, "Candy Cummings", in The Baseball Biography Project. Accessed 22 October 2007.
[2] I. Newton, Phil. Trans. R. Soc. 7, 3078 (1771-2).
[3] L. Rayleigh, Messenger of Mathematics 7, 14 (1877).
[4] R. Mehta, Ann. Rev. Fluid Mech. 17, 151 (1989).
[5] L. Briggs, Am. J. Phys. 27, 589 (1959).
[6] R. Watts and E. Sawyer, Am. J. Phys. 43, 960 (1975).
[7] J. Drury, "The Hell It Don't Curve," from The Fireside Book of Baseball, ed. by Charles E. Einstein (Simon and Schuster, 1956).
[8] R. Granger, Fluid Mechanics (Holt, Rinehart, and Winston, New York, 1985).
[9] P. Bearman and J. Harvey, Aeronaut. Q. 27, 112 (1976).
[10] R. Watts and R. Ferrer, Am. J. Phys. 55, 40 (1987).
[11] L. Alaways, Aerodynamics of the Curve-Ball: Investigation of the Effects of Angular Velocity on Baseball Trajectories, Ph.D. Thesis, University of California, Davis (1998).
[12] K. Borg, L. Soderholm, and H. Essen, Phys. Fluids 15, 736 (2003).