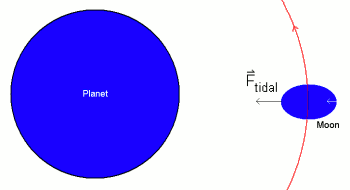
 |
| Fig. 1: Deformation of moon due to tidal force. |
This report summarizes the phenomenon of tidal heating, a mechanism by which an object's orbital gravitational energy and rotational energy is dissipated as heat. We first provide a qualitative discussion of a gravitational system exhibiting tidal heating and next present a more quantitative description of the dynamics of this process that includes some results for the amounts of heat so dissipated. Finally we apply this analysis to Jupiter's moons Io and Europa and Saturn's moon Enceladus and compare predicted and observed heating rates.
The tidal force on an object in an orbit around another object, say a moon around a planet, is a result of differing gravitational forces on the sides of the moon nearest and farthest from the planet. Using Newton's law of gravitation, we compute the tidal force on a moon of mass m and radius r around a planet of mass M and radius R:
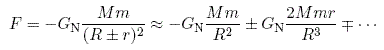
Where the second term in the series expansion gives the tidal force. If the moon is in a synchronous orbit around the planet - if its rotational and orbital periods are the same - then the differing forces on the near and far side of the moon distort its shape so that an initially spherical moon is now longer in the direction facing the planet than in the direction of its orbit (Fig. 1). The moon's orbit may become synchronous with the planet via the mechanism of tidal locking, by which an object's angular momentum about its axis of rotation is transferred to orbital angular momentum until the rotational and orbital periods match. For a discussion of this phenomenon and further references see Yeong Dae Kwon's report on this topic for this course.
This deformation involves heat dissipation through friction, as the interior of the moon must be rearranged in order for the deformation to occur. In order for heat to be dissipated continuously as a result of this deformation, the amount by which the moon is deformed must vary with time. If the eccentricity of the moon's orbit is nonzero, then the moon will be more deformed from a spherical shape nearer to the planet than farther from the planet since the tidal force on the moon scales with 1/R3. Thus the amount by which the moon is deformed is largest at the periapsis and lowest at the apapsis of its orbit and heat is dissipated continuously at a rate proportional to the square of the eccentricity (see analysis below) (Fig. 2).
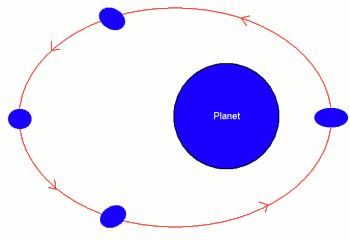 |
| Fig. 2: Deformation of moon at various points in orbit, eccentricity decays with time |
This heat dissipation tends to diminish the eccentricity of the moon and in turn the amount of heat dissipated by friction [1]. In order for the amount of heat dissipated continuously to not on average decay with the eccentricity of the planet's orbit on timescales longer than an orbital period, the moon's eccentricity must be maintained by gravitational interaction with another object. If the moon is in an orbital resonance with another moon - the ratio of the orbital periods of the moons is rational - farther from the planet, then the eccentricity of the inner moon's orbit will tend to grow in time as a result of its interaction with the outer moon. At equilibrium this rate of eccentricity growth is equal to the rate of decay due to tidal friction, so the inner moon is continuously heated at a constant average rate. Fig. 3 depicts a system exhibiting tidal heating of its moon.
The phenomenon of tidal heating was proposed as a possible heating mechanism since the 1970s, but the first calculation of its magnitude and dependence on various parameters of a gravitational system was done by Peale et al. in 1978 [2]. The following discussion is based closely on a simplified analysis by Meyer and Wisdom [3]. If the planet's mass is M, and the moon of mass m is in an orbit of eccentricity e and semimajor axis a, then the moon's angular momentum and energy are
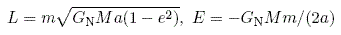
Now letting n = sqrt(GM/a3) and recalling that torque T is the time derivative of the angular momentum L, we write dE/dt = (dE/dL)*(dL/dt) ≈ nT, where we have ignored corrections of order e2. Now if a small torque results in an angular momentum change of ΔL for the system in time Δt, the resulting orbital energy change ΔE will be distributed in some way between the two satellites dE/dt = n0T0 + n1T1 = (d/dt)[E0+E1]+H, where 0,1 are subscripts referring to the two moons and H is the rate of heating, so at least one of the satellites is heated. Near a j:k orbital resonance, we have jn1 ≈ kn0 and so (1/n0)(dn0/dt) ≈ (1/n1)(dn1/dt). Now assuming that T0 >> T1 and n0T0 >> n1T1 and using these conditions at equilibrium we find
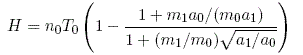
The torque on each satellite is given by [4]
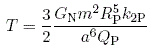
where k2P and QP are the potential Love number and Q of the planet. In equilibrium eccentricity e, the heating rate is then equal to [2]
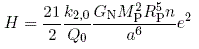
We see that the heating rate is proportional to the square of the moon's eccentricity. Using the above two expressions we can solve for e and find that e2 is proportional to (Q0/k20)*(kP0/QP0). Meyer and Wisdom summarize some methods for estimating these parameters for a moon around a planet.
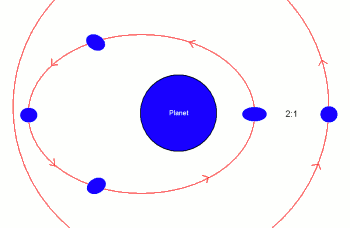 |
| Fig. 3: Moon in orbital 2:1 resonance is continuously tidally heated, eccentricity constant with time |
Enceladus is in a 1:2 orbital resonance with another of Saturn's moons, Dione, and so is a candidate to exhibit significant tidal heating. Squyres et al. [1] estimate the relevant parameters for Enceladus and concludes that tidal dissipation of heat is likely to be the only mechanism capable of melting the interior of Enceladus, as is evidenced by geologic observations of Enceladus'crust. Meyer and Wisdom provide a new estimate of the parameters involved and conclude that equilibrium tidal heating is insufficient to account for the heat rediated by Enceladus, but suggest that Enceladus may oscillate about this equilibrium, or that the quality factor Q of Enceladus may vary with temperature so that the moon is currently releasing heat that was stored during a previous phase of higher eccentricity [3]. Ojakangas and Stevenson discuss a mechanism for the episodic tidal heating of Enceladus in detail [5].
Jupiter's moon Io is among the most geologically active objects in the Solar System and is in a 1:2 orbital resonance with Europa. Peale et. al first proposed tidal heating in 1979 [2] as a mechanism by which Io's interior may have melted to produce ongoing geological activity. Subsequent models of Io suggest that it is nearly a rocky body heated within its body by solid state convection, but the ultimate source of heat remains tidal friction [6].
Voyager images of Europa along with spectroscopic UV evidence suggest the existence of a liquid ocean more than 100 km thick underneath this moon's crust. Aside from accretional and radiogenic heating, tidal heating has been suggested as a possible source of heat preventing this ocean from freezing [7]. Squyres et. al [7] calculate tidal friction to be a significant source of heat in Europa, while a more recent analysis by Ross and Schubert suggests that the effect is a marginal contribution to the heat that prevents the ocean from freezing [4]. Europa is a case of particular interest, as its liquid ocean may contain conditions similar to life-harboring hydrothermal vents in Earth's oceans.
© 2007 Dmitri Pavlichin. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] S. W. Squyres, R. T. Reynolds, and P. M. Cassen, "The Evolution of Enceladus," Icarus 53, 319 (1983).
[2] S. J. Peale, P. Cassen, and R. T. Reynolds, "Melting of Io by Tidal Dissipation," Science 203, 892 (1979).
[3] J. Meyer and J. Wisdom, "Tidal Heating in Enceladus," Icarus 188, 535 (2007).
[4] M. N. Ross and G. Schubert, "Tidal Heating in an Internal Ocean Model of Europa," Nature 325, 133 (1987).
[5] G. W. Ojakangas and D. J. Stevenson, "Episodic Volcanism of Tidally Heated Satellites with Application to Io," Icarus 66, 341 (1986).
[6] D. A. Rothery, Satellites of the Outer Planets: Worlds in their own right, 2nd Ed., (Oxford University Press 1999).
[7] S. W. Squyres, R. T. Reynolds, P. M. Cassen, and S. J. Peale, "Liquid Water and Active Resurfacing on Europa," Nature 325, 225 (1983).