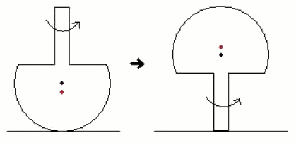
 |
| Fig. 1: The tippe top inverting. The black and red dot signifies the center of sphere and center of mass, respectively. |
The motion of gyroscopic bodies often baffle intuition. One famous example is the tippe top, which consists of a truncated sphere, flat on one surface, upon which a short rod is mounted. The tippe top is known for its counterintuitive behavior that after being spun rapidly enough with the stem upwards, the top refuses to sit on its rounded end, and proceeds to turn upside-down to rotate on its elongated stem, as in Fig. 1. Surprisingly, the center of mass is lifted after the inversion. This happens irrespective of the type of contacting surface, and seems to be independent of initial conditions. Moreover, this inversion phenomenon is a property of many spherical objects whose center of mass is displaced from the geometrical center of the sphere. I will now give a brief introduction to the theory of the top.
Del Campo (1955) demonstrated from a simple physical analysis that friction must be important in the behavior of the tippe top, which is summarized here. Let z be the axis perpendicular to the table surface. One observes that during inversion, the z component of the angular momentum is dominant, both before and after the inversion. Hence, the direction of rotation actually reverses with respect to coordinates fixed in the body of top. More importantly, after the inversion, the center of mass of the top actually elevates. This gain of gravitational potential energy necessarily comes from the loss of rotational kinetic energy, which implies the total angular velocity and total angular momentum in the z direction decrease during inversion. A reduction in the angular momentum Lz requires torques along the z axis. However, apart from friction, the only external forces acting on the tippe top are gravity and the normal force from contact with the table surface. Both these forces exert in the z direction, and cannot contribute to the torque required. Hence, a frictional force at the point of contact is critical in the explanation of the tippe top's intriguing behavior. The tippe top works since the center of mass is not the geometrical center of the sphere. Because the rotational axis (see Fig. 2) goes through the center of mass, the tippe top will slide over the surface on which it is spinning. This is our required source of friction.
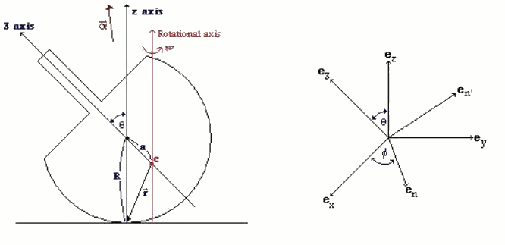 |
| Fig. 2: Tippe top and coordinate axes. |
We now present a simplified quantitative argument on why the tippe top tips over; this argument was first given by Pliskin (1954). As in Fig. 2, coordinates defined by the unit vectors ex, ey, ez are fixed in the laboratory frame. Making straightforward the argument of Cohen (1977), and keeping consistency with his notation, we define the new coordinate system en, en', e3 with the following equations:
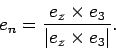
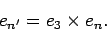
Using the Euler angles defined in Fig. 2, we can transform the two coordinate systems into each other:
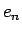 |
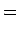 |
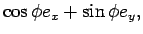 |
(3) |
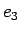 |
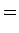 |
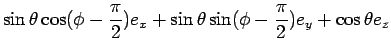 |
|
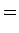 |
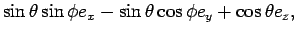 |
(4) | |
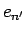 |
 |
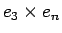 |
|
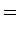 |
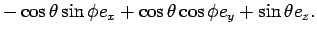 |
(5) |
Hence, we see from above that
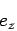 |
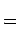 |
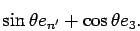 |
(6) |
The angular velocity α of the coordinate system en, en', e3 is then
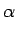 |
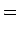 |
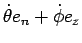 |
|
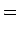 |
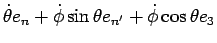 |
||
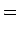 |
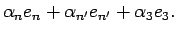 |
(7) |
Note that since we spin the tippe top rapidly, dφ/dt >> dθ/dt, and the top precesses rapidly as it slowly falls over. Hence, α points very closely to the positive z axis.
If we ignore the translation motion of the top, the frictional force Ff exerted at the contact point opposes the sliding motion of the top, hence Ff points along the -en axis. The torque Nf about the center of mass from Ff is
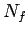 |
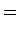 |
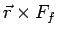 |
|
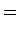 |
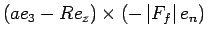 |
||
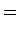 |
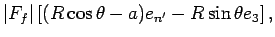 |
(8) |
where, as in Fig. 2, r is the vector from the center of mass to the contact point, α is the distance between the center of mass and the geometrical center, and R is the distance between the geometrical center and the contact point. Since the origin of our coordinate system en, en', e3 is the center of mass, gravity exerts no torque. Also, the torque from the normal force points in the en axis. Hence, our frictional torque Nf is the only torque that acts on about the en' and e3 axes.
In the beginning, 0 ≅ θ < cos-1(a/R), the torque about en' is positive and the torque about e3 is negative, so αn' increases and α3 decreases as time progresses. From eq. (7), the ratio α3/αn' = cos(θ) monotonically decreases with time, hence θ monotonically increases as the tippe top spins. When θ reaches cos-1(a/R) < θ < π/2, both the torques about en' and e3 are negative. However, the absolute value of the torque about e3 is larger, as one can check on the lower bound (R2 > a2) and higher bound (R > a) in this range. If the moment of inertia about the two axes are similar, the angular velocity α3 still decreases faster than αn', and θ will continue to increase. In the range π/2 < θ < π, both torques are still negative, so α3 and αn' still decrease with time, α3 becoming more negative since α3 = 0 at θ = π/2. From eq. (7), αn' = sin(θ) dφ/dt and α3 = cos(θ) dφ/dt, so the only way these angular velocities can continue to decrease is for θ to go on increasing, until the elongated stem finally touches the table. Then the situation is completely analogous to a conventional top, and the torque from the friction at the stem will tend to align angular momentum L with the z axis, pushing upright the top. This is why the tippe top tips and flips.
(c) 2007 Shih-Arng Pan. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] A.R. Del Campo, Am. J. Phys. 23, 544 (1955).
[2] W.A. Pliskin, Am. J. Phys. 22, 28 (1954).
[3] R. J. Cohen, Am. J. Phys. 45, 1 (1977).