The piano is a complex instrument capable of producing a wide range of tones and timbres. It is also large, expensive, difficult to calibrate and maintain, and of limited flexibility due to practical physical constraints. For these reasons it would be useful to have a computer model capable of emulating the piano which one could control with a lightweight digital controller. Here I demonstrate how one can create a realtime capable piano model based on physical principles using techniques of digital signal processing.
First we must understand the basics of how a piano works. The 88 keys of a piano are connected to weighted hammers. When a key is pressed a hammer is set into motion and it strikes a set of strings, from one string per note in the bass to three per note in the treble and high notes. The strings are terminated at one end by metal pins connected to a sturdy metal plate and at the other end by pins connected to a wooden bridge which vertically supports the strings and transfers the transverse motion of the strings to a wooden soundboard underneath the strings. The velocity of the soundboard in turn produce longitudinal pressure waves in the air which is the sound that are ears detect.
Before jumping into modeling, let us consider what aspects of the system are vital. All of the energy comes from the kinetic energy of the hammer. Most of the energy is stored in the transverse modes of the strings. Most of the loss in the strings occurs at the bridge, rather than from direct acoustic radiation, drag, internal heating or coupling to the frame. Most of the acoustic radiation comes from the bending motion of the soundboard. [1]
In most physical modeling problems, it is necessary to ignore some aspects of the system to keep the model simple and efficient. First, we are ignoring the coupling of the transverse string modes to longitudinal modes. The longitudinal speed of sound in piano strings is about 20 times that of the transverse oscillations, so the corresponding mode frequenices are 20 times higher. Humans can hear frequencies as high as about 20KHz, so we expect the longitudinal modes to be of perceptual importance for notes in the low range below a few hundred Hz. This is in fact the case, and it is the longitudinal modes that are responsible for the metallic sound of high velocity bass notes. Many pianos are tuned such that the longitudinal modes are in a roughly harmonic relation to the transverse modes, though, so the perceptual importance is greatly reduced. It is on these grounds that we can justify ignoring longitudinal modes. Another perhaps more cogent reason for ignoring them is the computational expense of modeling the nonlinear coupling. [2]
With less concern, we also ignore resonant modes of the piano case, coupling of strings to the frame, the distinction between the two polarizations of tranverse string oscillations normal and parallel to the soundboard, and coupling between non-unison strings. All of these factors have a minor effect on the quality of tones produced in the piano. [1]
The system has thus been reduced to the interaction between the hammer, the transverse string oscillations, the bridge, and the soundboard. The most straightforward way to model this system would be to write down a set of partial differential equations, spatially discretize the hammer in 0-dimensions, the string in 1 dimension, and the soundboard in 2-dimensions, and then use a finite difference scheme to integrate the system in time. [3,4] However this is computationally expensive and suffers from problems of stability and numerical dispersion. [5]
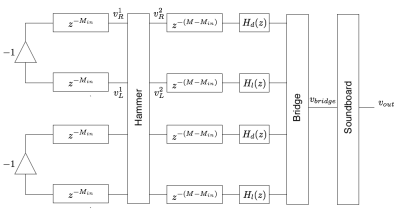
Instead, an efficient approach called digital waveguide synthesis will be used as the foundation of our model. Rather than attempting to integrate complicated partial differential equations which have all desired physical processes built in, the idea is to start with the simplest equation at the heart of the system: the 1-D wave equation for the strings. The solution can be efficiently implemented with delay lines without numerical error yielding results identical to finite difference methods. [6] We can then use techniques from digital signal processing and scattering theory to efficiently incorporate the effects of other terms in the equations. Figure 1 shows the structure of our model which will be explained in the subsequent sections.
The 1-D wave equation for transverse displacements y(x,t) on a non-stiff lossless string can be written
where K is the string tension and ε is the linear mass density in the string. The solutions of this equation are
for any twice-differentiable functions yR and yL with velocity
The interpretation is that the string supports right-going and left-going traveling waves at velocity c. We can take advantage of this interpretation by implementing the solution as a pair of digital delay lines, one for the spatially sampled right-going wave and one for the spatially sampled left-going wave. The value of y at any sampled point at any sampled time is the sum of the values at that point in the two delay lines:
where m is the spatial index, n is the time index, X is the spatial sampling length, and T=X/c is the temporal sampling time. In practice we set the scale by using a standard 1/T = 44100Hz.
For finite strings the length M of the delay lines is chosen so that N=1/(2Tf1) where f1 is the fundamental frequency of the string. Of course strings support modes above the fundamental frequency. For an ideal string with infinite impedance terminations, the displacement must be zero at either end of the string, so an integer number of half wavelengths must fit into the length L of the string. In other words the nth mode of the string has frequency
In order to keep piano strings relatively short, the propagation velocity must kept small by minimizing tension or maximizing linear mass density. Decreasing tension lowers the impedance of the string and upsets the impedance matching of the string and soundboard leading to poor transfer of energy. Decreasing tension also increases the amplitude of oscillations and thus losses due to drag and heat dissipation. Consequently piano strings are held at a tension near their breaking point. String lengths are instead kept manageably short by increasing the mass density and thus the radius of the string. This introduces stiffness into the strings, which can be modeled by adding a term to the wave equation [1]
where &kappa = ESG2 and E is the Young's modulus, S the cross section and G the radius of gyration of the string. The string is now dispersive, and the mode frequencies fn are stretched
where
The inharmonicity B is highest for the short strings in the high range. The mid range remains relatively harmonic, and the stiffness of bass strings is kept to a minimum by using wound strings rather than solid wire, resulting in intermediate inharmonicities.
Turning to the implementation of this inharmonicity, the frequency dependent phase velocity for stiff strings can be approximated [8]
To implement this in a digital waveguide, notice that the temporal sampling interval T=X/c(ω) is now a function of frequency so we must replace every delay element with a frequency dependent delay element
which is just an allpass filter. Allpass filters are linear time invariant, so to efficiently implement many of them in series we can decompose the series into a single delay line z-M and a single allpass filter with transfer function Hd. Together these linear elements can be made to approximate the desired phase delay. In practice we implement the dispersion filter with a Thiran allpass filter. [9] In general the delay lines must be shortened to compensate for the phase delay at the fundamental frequency introduced by the dispersion filter, and an additional fractional delay Thiran allpass filter must be inserted to tune the overall delay.
Note that it is the transverse velocity v(x,t) of the string at the bridge that drives the soundboard, not the displacement y(x,t). It is easy to show that an ideal string supports traveling wave solutions for v(x,t) as well, so the digital waveguide approach can be used unmodified.
The interaction of hammer and string is nonlinear and hysteretic. [10] We use a force model of the form
where F(u) is the restoring force acting on the hammer, u is the compression of the hammer felt, F0 is a measure of the stiffness of the felt, and &alpha is an effective hysteresis time. For real hammers u is on the order of 1mm, F0 ~ 70N/(mm)p, α~0.1ms, and p ranges from 2 to 4.
To incorporate this model into the digital waveguide requires relating the velocity of the hammer to the velocity of the strings at the contact point. [6] We integrate Newton's law for the hammer with du/dt = vhammer-vstring, dvhammer/dt = -F(u)/m. Scattering junction theory [8] then relates the outgoing string velocities at the junction to the load from the hammer and the incoming string velocities.
where Z is the string impedance and Ztot is the sum of the impedances meeting at the junction.
The finite bridge impedance is the primary loss mechanism, and it introduces modal decay times that vary with the inverse square of the frequency. The bridge coupling between unison strings is also important for reproducing the decay characteristics of the piano. [1]
In our model the strings for a given note are terminated at a scattering junction with one port representing the bridge with a frequency independent impedance about 1000 times greater than the string impedance. The transfer of energy from the soundboard back into the strings through the bridge is negligible and is ignored. The outgoing velocity at the bridge vbridge is then fed into the soundboard model.
We resort to phenomenological modeling of the soundboard due to its inherent 2 dimensional nature and the associated complexity of direct physical modeling. The soundboard acts roughly as a clamped diaphragm with an impedance that decreases with frequency and matches the impedance of air in the treble range. [4] Losses also increase with frequency, however resulting in a decrease of acoustic radiation in the upper treble. There is a sharp highpass cutoff frequency around 100Hz where the speed of bending waves in the soundboard equals the speed of sound in air. Resonances are densely spaced between about 50Hz and 200Hz with widely varying quality factors.
To qualitatively capture this behavior, we model the soundboard as a feedback delay network which efficiently implements the densely spaced modes. [12] The output vout(m) at time m is described by
where the yj are the outputs of the delay lines, and the delay times dk and feedback matrix Ajk are chosen to approximate the impulse response of a real soundboard. The constants bj and cj are chosen to minimize the coloration introduced by the network. [12]
We treated the bridge/soundboard impedance as frequency independent, but in reality the impedance is a complicated function of frequency. To model this physically requires expensive 2-D finite difference methods which incorporate the behavior of the ribs of the soundboard. [4] One finds that the primary effect is the introduction of variations in the frequency dependent losses in the strings which alter the decay rates of the string modes. The frequency dependent impedance also induces a frequency dependent phase shift and thus the string modes are slightly shifted.
The same phenomenon can be reproduced by matching seperately the frequency response of the soundboard and the decay rates of the strings and the soundboard. The frequency response of the soundboard is implemented with a small number of low order IIR biquad shaping filters in series with the feedback delay network. The variations in decay rates for string modes are approximate by inserting a first order IIR loss filter in series with the allpass dispersion filter in the digital waveguide. A loss filter with decay time characteristics of &tau(&omega) = 1/(c1+c3ω2) can be designed and in conjunction with the loss from the bridge impedance, the design gives good perceptual results. [12] The frequency dependent decay rate of the soundboard is implemented by inserting similar loss filters at the output of the delay lines in the feedback delay network. The phase shifts from the frequency dependent impedance can be absorbed into the allpass disersion filter.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Table 1: Wave files produced by synthetic piano code. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
The c code implementing this model can be found here. It does not generate realtime output but the algorithm is capable of ~10 note polyphony on a 1.5GHz processor.
In the upper part of Table 1, I show the outputs for various notes with an initial hammer velocity of 2.5m/s. The very low range suffers in quality in part because of the lack of longitudinal mode coupling and fine structure of the frequency dependent impedance of the soundboard. The mid range is reproduced rather well. The high notes, in particular the pesky A5, suffer mostly because of discrepencies between the impulse response of the feedback delay network and real soundboards.
In the lower part of Table 1, I show the results for A3 with various initial velocities demonstrating the dynamic characteristics of the model. As expected the higher velocity notes are louder and carry considerably more high frequency content at the attack.
© 2007 C. R. Otey. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] N. H. Fletcher and T. D. Rossing, The Physics of Musical Instruments (Springer, 1991).
[2] B. Bank and L. Sujbert, "A Piano Model Including Longitudinal String Vibrations," Proc. of the 7th Int. Conference on Digital Audio Effects, DAFx-4, Naples, Italy (2004).
[3] A. Chaigne and A. Askenfelt, "Numerical Simulations of Piano Strings. I. A Physical Model for a Struck String Using Finite Difference Methods" J. Acoust. Soc. Am. 5, 2 (1994).
[4] N. Giordano, "Simple Model of a Piano Soundboard", J. Acoust. Soc. Am. 102, 1159 (1997).
[5] J. Bensa et al., "The Simulation of Piano String Vibration: From Physical Models to Finite Difference Schemes and Digital Waveguides", J. Acoust. Soc. Am. 114, 2 (2003).
[6] J. O. Smith III, "On the Equivalence of the Digital Waveguide and Finite Difference Time Domain Schemes" http://arxiv.org/abs/physics/0407032, 2004.
[7] J. Bensa, S. Bilbao, R. Kronland-Martinet and J. Smith, "Computational Modeling of Stiff Piano Strings Using Digital Waveguides and Finite Differences" Acustica, 91, 289 (2005).
[8] J. O. Smith, "Physical Audio Signal Processing", http://ccrma.stanford.edu/~jos/pasp/, August 2007 Edition.
[9] J. Rauhala et al., "Tunable Dispersion Filter Design for Piano Synthesis," IEEE Signal Processing Letters, 13, 253 (2006).
[10] A. Stulov, "Hysteretic Model of the Grand Piano Hammer Felt," J. Acoust. Soc. Am. 97, 4 (1995).
[11] D. Rocchesso and J. O. Smith III, "Circulant and Elliptic Feedback Delay Networks for Artificial Reverberation'', IEEE Trans, on Speech and Audio, 5, 1 (1996).
[12] B. Bank, "Physics Based Sound Synthesis of the Piano", Masters Thesis, Helsinki University Of Technology Laboratory of Acoustics and Audio Signal Processing, 2000.