Inertial Navigation

We might think we already know what navigation is, but it's always useful to make sure we are on the same page before entering more complicated discussions. Navigation is defined by the Merriam-Webster dictionary as "the science of getting ships, aircraft, or spacecraft from place to place; especially : the method of determining position, course, and distance traveled" [1]. Navigation has always been a part of human activities. At first we relied on our senses and memory in order to get from one place to another, using familiarities in the landscape to guide our steps. When our journeys became longer, and we needed a more precise system we turned to the Sun, Moon, and other celestial bodies in order to determine our position. There was a point, however, when we could no longer rely on our senses and the need for more accurate sensors arose. Several gadgets were used for navigational purposes, including the astrolabe, the magnetic compass, clocks, etc. We will not go into detail about how and when they came about. Eventually we had both the theoretical and technical knowledge to be able to build inertial measurement devices, which we use in Inertial Navigation Systems (INS).

Throughout time, probably the most popular navigation method is dead-reckoning (originally dead-reckoning, for deduced reckoning). It works by using the actual position, direction, and speed in order to estimate the position at a later time, drawing the calculated trajectory in a map. In a way, INS works by the same principle, but instead it relies on the direct observation of the acceleration and rotation rates of an object and then using basic equations of motion in order to determine its position and altitude. Since the acceleration a is the second derivative of the position vector r, this is accomplished by integrating the measured acceleration of the object, taking into account its current altitude and initial position r_o and velocity v_o. This sounds very simple, and in principle it is, but a series of complications arise when we implement it. Later on we will discuss these difficulties.

There are mainly two types of INS: mechanized or gimbal-mounted systems, and strapdown systems. As their name states, gimbal-mounted systems use only accelerometers in a platform, or Inertial Measuring Unit (IMU), that is isolated from the object's rotations through a set of gimbals, thus maintaining a fixed orientation in an inertial reference frame. Three gimbals would technically suffice, but most systems use four in order to avoid what is called gimbal-lock, which happens when the axis of two of the gimbals are driven in the same direction, disabling their isolation capabilities. Mechanized systems use rotation sensing devices (gyroscopes), a feedback cycle, and an actuated platform, also keeping the IMU in a fixed orientation in an inertial reference frame. Strapdown systems use a combination of accelerometers and gyroscopes mounted in a platform rigidly attached to the object, using the output from the gyroscopes to compute the current attitude of the object.

Gimbal-mounted systems are difficult to implement due to the need of very high quality bearings, because even a little amount of friction can turn out to be disastrous for the system. On the other hand, mechanized INS have the advantage of having the accelerometers working in an inertial system, but the need for the actuators makes the system bigger, requires more power, and is often more expensive. Strapdown systems have higher computational needs, since they need to integrate the signals from both the accelerometers and the gyroscopes, compute the rotation that the object has undergone, and then the displacement. Historically, when stand-alone INS were used and needed high accuracy for extended periods of time, mechanized systems were implemented. There is a tradeoff when deciding whether to use mechanized or strapdown systems, and the outcome depends on the current state of circuit technology (crucial for strapdown systems) and sensors/actuators (important for mechanized systems), taking into account both cost and accuracy. Simple flowcharts for both mechanized and strapdown INS are shown [3]:

Fig. 1: Mechanized INS flowchart

Fig. 2: Strapdown INS flowchart

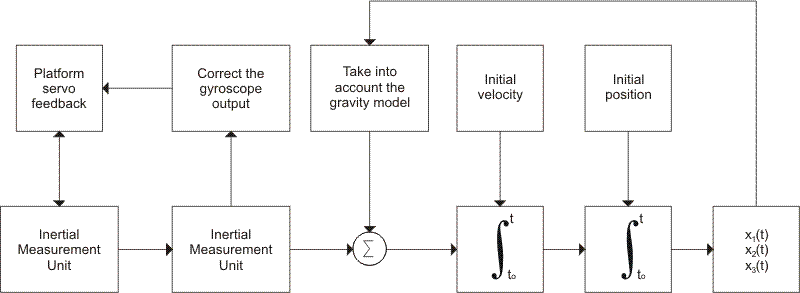
The basic equations needed in order to understand INS are explained below (here, I follow the notation in [4]). First, our accelerometers will give us a measure of what is called the specific force:

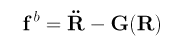
where the superscript b indicates that it is measured in the body reference frame, R is the inertial position vector of the proof mass our accelerometer uses, and G(R) is the position-dependent gravitational acceleration. However, we need to translate this into an external inertial reference frame, so we use the transformation matrix T:

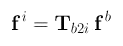
where the subscript b2i indicates that it transforms from the body reference frame into our external inertial reference frame. But this transformation matrix changes with time, due to the rotation of the object,

where

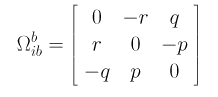
is the skew-symmetric form of the angular velocity of the body ω^b_ib (the rate of angular rotation between the body's frame and the external inertial frame, coordinatized in the body's frame), and is meant to be used in cross products ( Ω^b_ib=ω^b_ib × ). In component form, ω^b_ib= [ p, q, r ].

Fig. 3:Piezoelectric accelerometer.

At this point we integrate and obtain the object's current velocity and position (in the external inertial reference frame), and if we wish to use a different reference frame then it's straightforward from here.

The Eyes and Ears of INS: Accelerometers and Gyroscopes

Accelerometers are, as their name indicates, acceleration sensors. There is a wide variety of accelerometers, differing in the way they measure the acceleration, their range and accuracy. For example, there are mechanical accelerometers that measure the position of a test mass coupled to a spring; piezoelectric accelerometers that measure a change in voltage due to the compression of a piezoelectric crystal; and a series of microelectromechanical (MEMS) that rely on various principles for their operation but share their scalability and miniaturization. In the following lines we will describe the functioning of some of these devices.

Nemirovsky et al. [8] designed an accelerometer based on the piezoelectric effect (voltage/charge response to mechanical stress). In their device, a thin film of piezoelectric material is held between a test mass and a substrate. When subject to acceleration along its sensitive axis (marked as the arrow in Fig. 3) the piezoelectric material is subject to stress due to its coupling to the test mass, and the generated charge is sensed and then processed in order to produce the sensor's output.

Fig. 4: MEMS accelerometer.

Fig. 5: MEMS accelerometer.

Fig. 6: MEMS accelerometer.

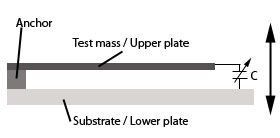
Boser and Howe [7] describe a set of surface micromachined accelerometers, and here I present the proposed designs for two of them. The operating principle of such accelerometers is measuring the variation in capacitance caused by the motion of the proof mass. One of them, depicted in Fig. 4, is sensitive to out-of-plane accelerations (marked with the arrow), while the other one (Fig. 5) is sensitive to acceleration in one of the in-plane axes.

In the first device, the capacitance between the proff mass and the substrate is larger (mainly due to the larger area) than in the second one, and measuring the variations in it is easier but there are potential asymmetry issues, having a better performance with small displacements.

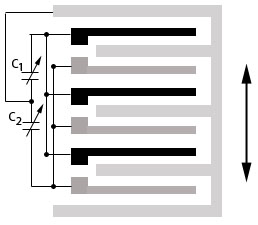
Modeling the capacitance in the second device is more complicated due to the effect of fringing fields, and its sensitivity is limited in the small-displacement regime.

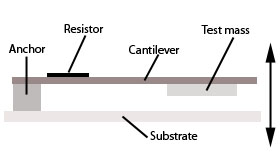
Roylance and Angell [6] designed an accelerometer consisting of a silicon beam with a p type resistor on top. When the device is accelerated in the direction normal to the surface of the silicon beam, the beam bends and a change in resistance is measured. A second resistor is included for the correction of temperature-caused variations in resistance. In Fig. 6 a very conceptual sketch of the device is shown.

Originally the term gyroscope was used for describing a device invented by Leon Foucault, consisting of a rapidly rotating disk with a heavy rim, which was mounted in a set of low-friction gimbals (Fig. 7). This was part of Foucault's effort to study Earth's rotation, along with the experiment that showed the rotation of the plane of oscillation of a pendulum. Now we understand for "gyroscope" any device that is used to measure the rotation θ (or the rate of rotation ω) of an object, and their design and functioning is very diverse. In the following lines we will briefly describe a few of them.

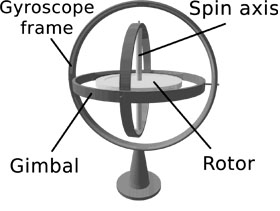Fig. 7: Original gyroscope [14].

Fig. 8: Vibrational gyroscope.

Fig. 9: Optical gyroscope.

Several gyroscope designs use the fact that a combination of turning rate and Coriolis effect couple different vibrational modes of the sensing structure. The system is driven in one vibrational mode and then sense the undriven mode, which is an indicator of the rotation rate. A basic design is shown in Fig. 8, but it could also use vibrating beams or wires, tuning forks, cavities, or more complicated structures as presented by Weinberg and Kourepenis [9], Chen et al. [10], and Xu et al. [11].

Optical gyroscopes are radically different compared with mechanical gyroscopes. They used the Sagnac effect, which arises when a beam of light travels along a closed path. If the loop then rotates with respect to an inertial reference frame, the actual length traveled by light going in opposite directions inside the loop differs (in order for the beam to return to a fixed point in the rotation loop). This is detected using interferometric techniques and the rotation rate can be determined. Since the sensing device relies on light and not an inertial property in order to measure rotation, it has a better performance than mechanical gyroscopes in a non-stabilized environment, such as strapdown IMUs.

Such gyroscopes can be built using mirror arrays, fiber optic loops, or lasing cavities. There is a great amount of literature containing a more detailed description of the functioning and design of these devices [5, 12, 13].

Sources of Error

INS are very complex systems, so there is a large variety of possible errors that should be accounted for. These errors could be due to the sensors (accelerometers and gyroscopes), or in the processing unit, for example. A more detailed (but by no means complete) list of the incurred errors is below:

• Noise in the sensor signals.
• Errors in the sensing devices, such as: bias, nonlinearity, scale factors, asymmetry, dead zones, quantization. These types of errors are represented in Fig.
• Sensor misalignment, resulting in non-orthogonal axis in the object's reference frame. Controllable by using more than the minimum number of sensors (redundancy).
• Imprecise gravity model. Since gravity has to be accounted for in the accelerometer's measurements, if the used model is not precise it will result in navigation errors.
• Numeric computation error. The numerical integration carried out when calculating the object's velocity and position is bot perfect, and several errors result by approximating an integral with a finite-interval sum.
• Analog-to-digital conversion error. When converting sensor output from analog signals into digital ones that will be fed into the navigation computers, there is room for error, quantization being the most common one.
• System initialization errors. The INS needs initial parameters for the object's position, attitude, and velocity. If such input is not correct it will affect the system's accuracy.

What about GPS?

As we have seen, while INS are standalone systems, they do not work well for long periods of time, due to the accumulation of error. Global Positioning Systems (GPS) rely on a network of satellites and in the triangulation of their signals in order to calculate the position of the receiver. This works very well, with accuracies on the order of 10m (main sources of error in GPS are discussed in [5]), but the downside is that the receiver needs to be able to detect the signals from at least three satellites, thus limiting its applicability in heavily forested areas, underwater navigation (like submarines, ocean floor mapping, and others), underground positioning (inside a mine shaft or a tunnel, for example), and in some extremely rugged terrains (naturally or man-made). Also, GPS provides information about the position, but not the attitude, of the object in question. In the field of military applications, relying too much on GPS is potentially dangerous, since the satellite network could be intentionally or accidentally shut down or jammed, crippling the navigation capabilities of missiles, for example.

As we can see, neither INS nor GPS are the unique solution to our navigation needs, but they can be used together in what is called aided systems, combining the strengths of each one in order to overcome the other's weaknesses. One such system is that which uses INS for the main navigation algorithms, but from time to time receives input from a GPS receiver, correcting and compensating for the error in the INS.

Other applications of IMUs

Geodesy pertains to the determination of coordinates for points on Earth's surface. Thus, using INS (or more precisely, IMUs) in order to calculate the position along a path is useful for this sense. However, the level of accuracy expected for geodetic measurements is on the order of 10^-2m of better, so INUs need to be used with a lot of external information if we are to be able of correcting errors. One of the particular uses along this line is in the Inertial Survey System, using inertial measurements to determine point coordinates in a geodetic network.

If we combine the accuracy of GPS in determining the position of an object and the capabilities of IMUs for sensing forces it is possible to map the gravitational field above Earth's surface. This can be later be analyzed and related to probable mineral or petroleum deposits, and also used for improving the gravity model used in compensating INS measurements in later missions [5]. This approach doesn't combine GPS and INS in order to correct each other's inaccuracies; rather, it takes advantage of the different functioning of them in order to use their outputs to calculate the gravity field, thus combining the errors from both GPS and INS.

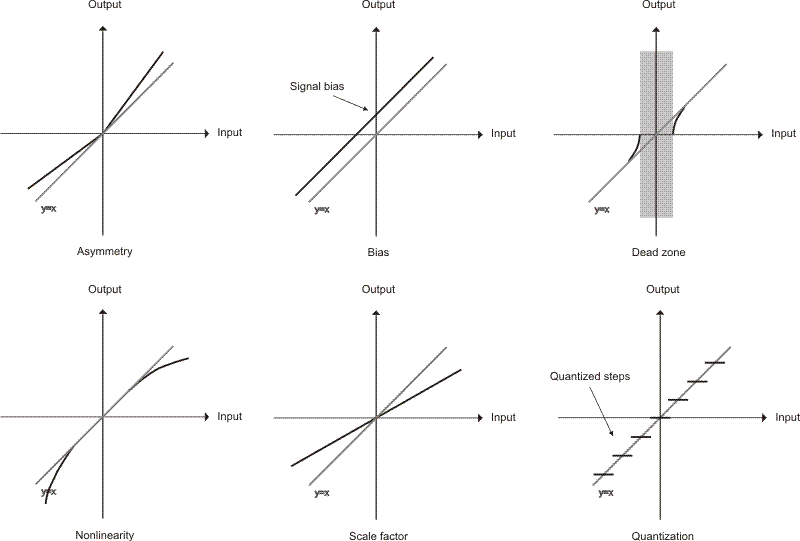Fig. 10: Types of sensor errors [3]

© 2007 R. J. Noriega-Manez. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.

References

[1] Merriam-Webster.(2006-2007). Merriam-Webster online dictionary. Retrieved October 26, 2007, from http://www.merriam-webster.com/dictionary/navigation.

[2] S. T. Thornton and J. B. Marion, Classical Dynamics of Particles and Systems (Thomson Brooks Cole, (2004).

[3] M. S. Grewal, L. R. Weill, and A. P. Andrews, Global Positioning Systems, Inertial Navigation, and Integration (Wiley-Interscience, 2001).

[4] J. A. Farrel and M. Barth, The Global Positioning System and Inertial Navigation (McGraw-Hill, 1999).

[5] C. Jekeli, Inertial Navigation Systems with Geodetic Applications (de Gruyter, 2001).

[6] L. M. Roylance and J. B. Angell, "A Batch-Fabricated Silicon Accelerometer," IEEE Trans. Elec. Dev.26, 1911 (1979).

[7] B. E. Boser and R. T. Howe, "Surface Micromachined Accelerometers," IEEE J. Solid-State Circuits 31, 366 (1996).

[8] Y. Nemirovsky et al., "Design of Novel Thin-Film Piezoelectric Accelerometer," Sensors and Actuators A: Physical 56, 239 (1996).

[9] M. S. Weinberg and A. Kourepenis, "Error Sources in In-Plane Silicon Tuning-Fork MEMS Gyroscopes," J. Microelect. Sys. 15, 479 (2006).

[10] Y. Chen, et al., "A Novel Tuning Fork Gyroscope with High Q-factors Working at Atmospheric Pressure," Microsys. Technol. 11, 111 (2005).

[11] Y. Xu et al., "A Monolithic Triaxial Micromachined Silicon Capacitive Gyroscope," Proc. 1st IEEE Intl. Conf. on Nano/Micro Engineered and Molecular Systems (2006).

[12] V.E. Prilutskii, "High Precision Fiber Optical Gyroscope with Linear Digital Output," Proc. 5th Intl. Workshop on Laser and Fiber-Optical Networks Modeling, 259 (2003).

[13] C.Riedinger and S.Lecler, "Optical Sagnac Gyroscope: An Approach of Automobile Applications," Proc. SPIE 6198, 61980E (2006).

[14] K. J. Walchko, "Low Cost Inertial Navigation: Learning to Integrate Noise and Find Your Way," M.S. Dissertation, University of Florida (2002).

[15] Gyroscope. (2006, October 4). In Wikipedia, The Free Encyclopedia. Retrieved October 30, 2007, from
http://en.wikipedia.org/wiki/Image:3D_Gyroscope.png.