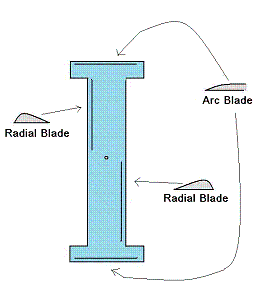
 |
| Fig. 1: Blades of a typical boomerang. |
A boomerang is a flying device known for returning to its initial position of the throw. A typical boomerang consists of two types of blades - radial blade and arc blade - arranged in a plane, as shown in Fig. 1. Usually, a boomerang is held almost vertically on launching by the tip of one of the blades, and it is thrown toward the horizon or in a slightly upward direction. In this way, the boomerang has initial translational and rotational motions, and the combination of these two motions determines its flight path.
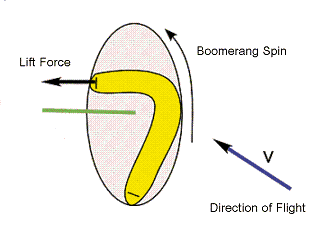
When the boomerang spins around its center of mass, radial blades and arc blades are activated alternately and interact with air (Fig. 2). This produces two types of gyroscopic precessions.
The first type precession is responsible for boomerang return. When the radial blades are in active position, lift forces are produced by air flow on both forward and backward spinning sides of blades (Fig. 3a). Lift force is due to Coanda effect, and for lift coefficient Cy, air density ρ, wing area A, and velocity v, it is given by the following formula:
Since the velocities of the forward spinning blade and backward spinning blade are different, the lift forces exerted on the two sides have different magnitudes. This results in boomerang precession around z-axis with angular velocity Ω 1, as shown in Fig. 3b. Due to this first type precession, the boomerang turns backward. [2]
The second type precession makes the flight time longer and determines the trajectory pattern. As the translational speed of the boomerang decreases, the vertical component of the lift force decreases as well. Through the second precession, the arc blades keep the boomerang continuously rotating and thus maintain constant lift force. The arc blades have either negative or positive angle of attack. When they become active and the radial blades are parallel to the direction of the flight, the lift force generated by the arc blades results in the precession around x-axis with angular speed Ω2 (Fig. 4a, 4b). Arc blades' angle of attack determines the sign and value of Ω2. [2]
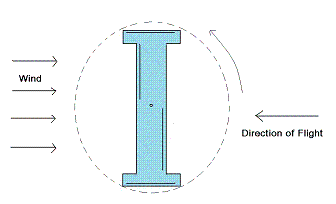 |
| Fig. 2a: Radial blades are active, arc blades passive. |
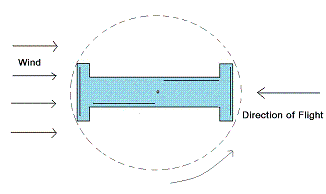 |
| Fig. 2b: Arc blades are active, radial blades passive. |
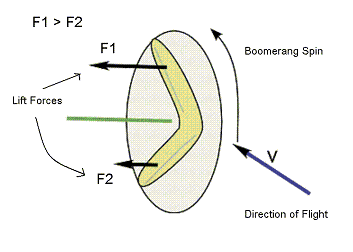 |
| Fig. 3a: Lift forces generated by radial blades. |
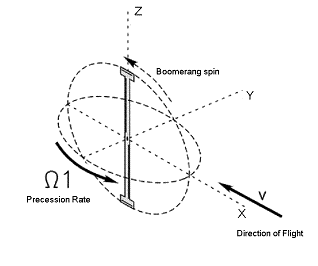 |
| Fig. 3b: First type gyroscopic precession. |
The flight trajectory is determined by the coefficient K in the relation
When K is about 1/3, the boomerang has "8" type flight pattern, and when K is about 1/4, it has "O" type trajectory. If K << 1/4, the boomerang is oriented vertically for too much time and falls down in ballistic trajectory. In the case K >> 1/3, it flies with corkscrew trajectory and does not return.
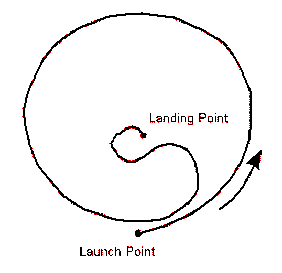
"8" type flight trajectory is shown in Fig. 5. In this type, the boomerang executes a 180 degree turn to the left reversing its forward flight. Then, it rotates 90 degrees hovering closely to the launch point. As it passes the launch point, it follows a second small loop to the opposite side. Therefore, the total flight pattern looks like an asymmetrical "8".
Fig. 6 shows the circular "O" type trajectory. After a forward flight, the boomerang makes a 270 - 360 degree turn to the left, and reverses its direction of flight. Similarly to "8" type, it then rotates 90 degrees from vertical and returns to the point of the launch. As it passes the launch point, it continues to fly a second small loop to the same side. The total flight pattern is thus helix type and looks like "O".
More complete theoretical analysis is conducted in the paper by Azuma [1]. We assume that 1) the boomerang is a rigid body without any elastic deformation during the flight. 2) the induced velocity is homogeneous over the rotational plane where its magnitude is determined by the momentum balance with respect to the time-averaged aerodynamics thrust over one period. Then, the aerodynamic forces and moments can be derived applying blade element theory based on the quasi-steady lifting-line theory. The equations of motion of the boomerang (which are nonlinear) are obtained by summing the aerodynamic, gravity, and inertial forces and their moments, as shown in Azuma's paper [1].
 |
| Fig. 4a: Lift force generated by arc blades. |
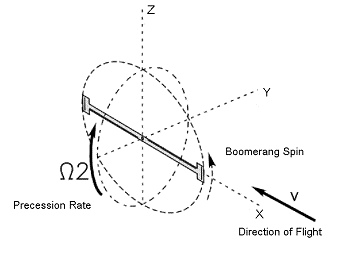 |
| Fig. 4b: Second type gyroscopic precession. |
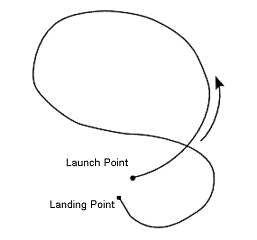 |
| Fig. 5: "8" type flight. |
 |
| Fig. 6: "O" type flight. |
By the Runge-Kutta method, the equations of motion can be solved numerically, and the results of numerical simulations are presented in Azuma's paper [1]. The qualitative behaviors of the typical returning boomerang are characterized as follows. Firstly, a short-period oscillation, with the same frequency as that of the spin about vertical axis of a blade, occurs with strong pitching and rolling motions. The amplitude of the oscillation increases in ascending flight and decreases in descending flight. This oscillation is caused by an asymmetry in the aerodynamic moment associated with a large reversed-flow region due to a large moment of inertia.
Secondly, a long-period oscillation originates from the exchange of potential energy with kinetic energy. Although the boomerang's linear kinetic and potential energies decrease throughout the flight, the rotational energy does not decrease as much due to the second gyroscopic precession by the arc blades. Therefore, the total energy change comes mainly from the change of the kinetic and potential energies, and the slow interchange between the two types of energies results in a damped phugoid oscillation.
When the boomerang passes near the site of initial takeoff, it makes a short, near hovering flight and lands softly. Because its forward velocity is low, the relative speed and angle-of-attack distribution are homogeneous over the rotational plane. The flight speed reaches the local minimum before the landing, letting a human catch the boomerang easily.
The motion of a returning boomerang is governed by the lift forces and gyroscopic precessions, which are produced by radial blades and arc blades. The ratio between the angular velocities of first and second type precessions determines boomerang's flight pattern. Numerical analysis shows further that both short-period oscillation and long-period oscillation are present during the flight.
© 2007 Yong Suk Moon. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] A. Azuma et al., "Flight Dynamics of the Boomerang, Part 1: Fundamental Analysis," J. Guid. Cont. Dyn. 27, 545 (2004).
[2] S. Pakalnis, "Aerodynamics of Boomerang," Research Support Technologies, April 2006.
[3] M. Battipede, "Boomerang flight mechanics: Unsteady Effects on Motion Characteristics," J. Aircr. 36, 689 (1990).
[4] F. Hess, "The aerodynamics of boomerangs," Sci. Am. 219, 124 (1968).
[5] A. L. King, "Project Boomerang," Am. J. Phys. 43, 770 (1975).