Tidal Acceleration in the Earth/Moon System

Introduction

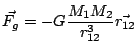
This paper is about the two-body gravitational problem and focuses on the effect that tidal forces between the two bodies can have on their overall orbits. I find it helpful to keep a concrete example in mind and will focus on the Earth/Moon system, which provides a helpful example for several reasons. First, the Moon is massive enough and close enough that it exerts a strong tidal force on Earth, perhaps most dramatically demonstrated by the ocean tides. Additionally, the Earth/Moon distance has been very accurately measured (to within a few centimeters) by laser ranging since 1969 and the length of Earth's day can be inferred from the fossil record as far back as 620 million years ago. Finally, the Earth/Moon system can be very accurately modeled by Newton's formulation of gravity

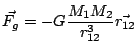
A consequence is that possible trajectories for the two-body system are simply the conic sections and can take the form of either ellipses for bound orbits or hyperbolas for unbound ones. Parabolic trajectories represent a borderline case between these two. It is easiest to derive this relation by assuming that the physical sizes of all the gravitating bodies are negligible and to limit the discussion to interactions between point particles. While this approximation is very useful, my consideration of tidal forces will need to recognize the fact that planets and other satellites are deformable bodies of finite size rather than structureless point particles. This means that the satellites might not have perfect spherical symmetry and that they might, accordingly, be subject to torques and precessions as they follow their otherwise elliptical trajectories through spacetime.

Eccentricity of Earth

If we are no longer treating the Earth to be a point particle, we can think of it instead as a flattened speroid of constant density with a bulge at its equator due to its rotation. To estimate the flattening, we can suppose that the Earth is made of a very viscous fluid and that the centrifugal acceleration at the equator should therefore be balanced by the difference in the gravitational accelerations at the equator and the poles.

The acceleration due to gravity at the poles and equator is

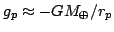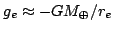where r_p and r_ε is the equatorial radius. If we assume that the long-term behavior of the Earth is like that of a fluid, the difference between these accelerations should be the centrifugal acceleration Ω²r_ε, where Ω is the angular velocity of rotation of the earth. We can therefore obtain our guess at the eccentricity of the earth:

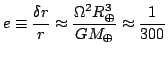
This estimate, of course, is rather crude because it presumes a spherically symmetric gravitational field to begin with and because it neglects other effects.

Distortion and Acceleration

Another effect tending to distort the Earth is the differential pull of the Moon's gravity on the Earth; this is known as a tidal force and it will tend to stretch the Earth along the Earth/Moon axis, flattening the Earth in both perpendicular directions. Because the Earth's crust exhibits a tremendous amount of friction in response to this stretching and because the Earth spins at a faster rate than the orbital speed of the moon, however, this bulge does not lie directly below the moon, but is instead always ahead of the Earth/Moon axis. This asymmetry means there will be a net torque, in addition to a force, on Earth due to Moon's gravity!

In the case of the Earth/Moon system, where the moon orbits in the direction of Earth's rotation, and where Earth's rotation is faster than the orbital frequency of the moon, the effect of this torque will be to slow Earth's rotation, lengthening the day. In accordance with Newton's third law, an equal and opposite torque must act on the Moon, increasing its orbital angular momentum, thereby increasing the length of the month. This process must continue (however slowly) until Earth's day and month are equal, at which point the Moon will never seem to move in Earth's sky and Earth is said to be tidally locked to the moon. It is important to note that, while this process does conserve angular momentum, it does not conserve energy, which is dissipated by frictional heating in the Earth's crust. Circular orbits have the lowest energy for a particular angular momentum, so the process also leads to a circularization of the orbits, in addition to their locking.

I should comment that the reverse effect has already happened; the Moon is tidally locked to Earth and there is a "dark" side of the Moon which cannot be seen from Earth's surface.

If we write the law of conservation of angular momentum for the Earth/Moon system, we have

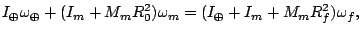
while Kepler's Law requires that

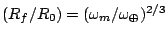
In these equations, I represents a moment of inertia, ω_⊕ is the angular rotation of the Earth about its own axis, and ω_m is the orbital angular speed of the Moon about the Earth. If we approximate both the Earth and Moon as perfect spheres, then I=(2/5)MR² and we have

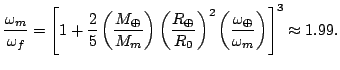
So the final month and the final day on Earth will both be just over 1400 SI hours, or nearly 60 of today's days!

Experimental Verification

While it is possible to calculate the final angular velocities in the Earth/Moon system, it is difficult to estimate the rate at which these velocities change without a detailed understanding of frictional heating in the Earth's core. Worse, measurements of the length of Earth's day are complicated by competing effects which tend to shorten the day. The most important such effect is likely to be fact that Earth's poles were flattened by an accumulation of ice during the ice age and, though this ice is now gone, Earth's shape is still being slowly restored.[1] This causes a continual decrease in Earth's moment of inertia, increasing Earth's rate of rotation, thereby shortening the day.

Nonetheless, changes in the Earth/Moon distance can be accurately observed today and this distance is indeed increasing at a rate of 3.84±0.07 meters per century.[2] Furthermore, there is paleontological evidence that the Earth rotated faster in the remote past; 620 million years ago, the day was 21.9±0.4 hours![3]

© 2007 Mike McCourt. The author grants permission to copy, distribute and display this work in unaltered form, with attributation to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.

References

[1] W. R. Peltier, "Ice Age Geodynamics," Ann. Rev. Earth. Planet. Sci. 9, 199 (1981).