Spring Gravimeters and Other Alternatives

Fig. 1: Diagram of the Spring Gravimeter

Introduction

The ideal-spring gravimeter, which uses a superconducting sphere, and other gravimeters will be discussed. A gravimeter is an instrument used to measure specific gravity or variations in a gravitational field that occurs as a result of position on the globe. The acceleration of gravity, g (not the gravity constant G) will be covered in this article. The gravimeter is an essential tool in geophysics and metrology, and it has many applications, such as oil exploration, mineral exploration, and precision inertial navigation. Depending on the method of the gravity measurement, gravimeters are classified as "spring-based relative gravimeters" and "absolute free-fall gravimeters." Spring-based relative gravimeters measure only relative gravity in accordance with the response of a spring. Absolute free-fall gravimeters measure g, the acceleration due to gravity by a free-falling retroreflector or free-falling atoms. This article discusses all these gravimeters in terms of performance. The main factors that determine the performance of gravimeters are sensitivity, drift and accuracy. In addition, cycle time, mobility and measurement method are important factors, depending on the application.

Spring-based Relative Gravimeters

Spring gravimeters and ideal-spring gravimeters are spring-based relative gravimeters. A spring gravimeter (LaCoste-Romberg gravimeter [1]) has good sensitivity even on a mobile platform, but it needs regular recalibration and has the limitations of a mechanical spring, such as aging. An ideal-spring gravimeter (superconducting gravimeter [2,3,4]) has the best sensitivity relative to the other gravimeters. However, the ideal-spring gravimeter is limited by the environment, and it is difficult to use on a mobile platform.

Spring Gravimeter (LaCoste-Romberg Gravimeter)

Using a zero-length spring, we can implement a LaCoste-Romberg gravimeter. A zero-length spring has no extension corresponding to zero initial force. This spring uses a linearized stress-strain curve around the origin; the length of the spring is directly proportional to the external force. The acceleration of gravity, g is measured at the equilibrium state. The temperature-controlled zero-length spring sustains a mass against gravity, and gravity variations change the spring's length. Important errors arise from the cross coupling between horizontal and vertical accelerations and a gravimeter's imperfections. Most of these errors can be corrected by using a dynamically stabilized platform. The platform provides highly accurate gravity measurements from a moving ship or aircraft. A spring gravimeter is a compact transportable system that has good sensitivity (1 x 10^-10 gHz^-1/2) and drift rate (δg/g = 3 x 10^-8 day^-1). The non-ideal mechanical spring always needs recalibration, and most drift comes from the aging of the spring, which changes the spring constant.

Fig. 2: Diagram of the cryogenic portion of the Ideal-spring Gravimeter

Ideal-spring Gravimeter (Superconducting Gravimeter)

A superconducting sphere is the best candidate for replacing a mechanical spring with an ideal spring. The sensitivity is up to 10^-12 g Hz^-1/2, and the drift rate is about δg/g = 2 x 10^-10 day^-1. Superconductivity occurs when the superconducting material goes below a sufficiently low temperature, such as a few degrees Kelvin. Below the critical temperature, currents move through the material without dissipation. Depending on the zero resistance property of superconductors, the newly generated magnetic field from a persistent current causes an applied external magnetic field to be excluded from the inside of the sphere. The magnetic levitation force, which can lift the superconducting sphere, comes from the interaction between the inhomogeneous magnetic field of the coils and the persistent currents induced by it in the superconducting sphere. On the vertical axis, there are two Helmholtz-type coils which levitate the superconducting sphere above the plane of the upper coil. The superconducting sphere trapped in the inhomogeneous magnetic field is working as the ideal spring because of repulsive magnetic force. The ideal-spring superconducting gravimeter has perfect stability, which comes from the stability of the persistent currents.

The position of the sphere is measured by a magnetic flux detector and six capacitor plates. A magnetic flux detector at the bottom of the chamber detects variation of the vertical magnetic field. The measured capacitance between the sphere and the capacitor plates provides the precise position of the sphere. Based on the measured position of the sphere, the total levitating force and the force gradient can be adjusted by the magnetic levitation. We can control the position of the sphere and the restoring force on it. Hence, the sphere can be supported and be made responsive to a small change in gravity.

The sensitivity of a gravimeter composed of a superconducting sphere is expected to be much higher than that of a spring gravimeter. The performance of the ideal-spring gravimeter on a moving platform is limited even though the variations of the sphere in gravity are counter-balanced using force feedback. When the instrument is moved, vibration-induced magnetic flux-jumps in the superconductor cause gravity offsets in the gravity reading.

II. Absolute Free-fall Gravimeters

Falling corner-cube gravimeters [5] and atom interferometer gravimeters [6,7] are absolute free-fall gravimeters. These absolute free-fall gravimeters can also be used for measuring the gravitational constant G [8]. The corner-cube absolute free-fall gravimeter has the best accuracy of the gravimeters, but its mechanical structure for repeated free-falling prevents its use on a mobile platform and limits its cycle time. The atom interferometer gravimeter has good accuracy with a fast cycle time and a high mobility relative to other gravimeters.

Fig. 3: Falling Corner-cube Gravimeter

Falling Corner-cube Gravimeter

A laser interferometer monitors the motion of a freely falling corner-cube retroreflector in a vacuum. The interferometer detects optical fringes which come from optical interference. This signal is used to determine the local acceleration of gravity. This falling corner-cube gravimeter is an absolute free-fall gravimeter. When the drop rate is about 1/15 Hz, the sensitivity is 5 x 10^-8 g/Hz^-1/2 and the accuracy is δg/g = 2 x 10^-9. As the drop rate becomes higher, vibration-induced accuracy degradation occurs. The sensitivity and accuracy strongly depends on place and drop rate. The sensitivity and accuracy are comparable to those in the atom interferometer gravimeter, but the falling corner-cube gravimeter has some limitations in terms of mobility due to its mechanical dropping platform.

Atom Interferometer Gravimeter

An atom interferometer gravimeter with a sequential light pulse [5,6] can be implemented by an atomic-fountain interferometer. It has good sensitivity and good accuracy (about 4.2 x 10^-9 g/Hz^-1/2 and &deltag/g = 3 x 10^-9. It also has fast cycle time (1.3 sec). Laser-cooled wave packets of cold atoms are sequentially exposed to π/2-π-&pi/2 pulse beams. The principle is similar to that of an optical interferometer. For deBroglie matter waves, i.e., cold atoms, a π/2 pulse works as a beam splitter, and a π pulse works as a reflector. Cold atoms with an initial state are prepared at the bottom of the chamber, and the atoms are launched upward. The first π/2 pulse at t₀ creates a superposition of states |1> and |2>, and the atomic beams are split as shown in position 1 (Fig.4). The atoms are almost stopped at the top of the chamber because of gravity. The second π pulse beams at t₀ + T deflect each partial atomic beam in opposite directions at positions 2 and 3. The atoms fall towards the starting position. The third π/2 pulse beams at t₀ + 2T recombine the two partial atomic beams, which causes the atomic wave packet to interfere with the other states' atoms as shown in position 4. The atomic phase difference along the different paths allows the determination of g, the acceleration due to gravity. In addition, the limited stabilization of laser frequency and phase limit the precision of atom interferometer gravimeter.

Fig. 4: Light-pulse Atomic Interferometer.

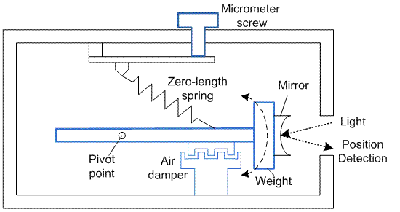
III. Performance Comparison

A spring gravimeter has good sensitivity and good transportability, but it has the limits of a mechanical spring and low cycle time. An ideal-spring gravimeter overcomes the problem of a spring gravimeter allowing greater sensitivity, but it is difficult to use the gravimeter on a moving platform. In addition, both gravimeters are spring-based relative gravimeters which cannot measure the absolute value of gravity; the performance factor, accuracy, is applicable only to absolute free-fall gravimeters.

A falling corner-cube gravimeter and an atom interferometer gravimeter have good sensitivity and accuracy, and both are absolute free-fall gravimeters. A falling corner-cube gravimeter has limited mobility and low cycle time due to its repeatedly falling retroreflector. The performance of an atom interferometer gravimeter is limited by the limited stabilization of laser frequency and phase, but it has good mobility and high cycle time, which could be applied to precision inertial navigation sensors.

Gravimeter Comparison Chart

© 2007 Jongmin Lee. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.

References

[1] L. Lacoste, N. Clarkson and G. Hamilton, "Lacoste and Romberg Stabilized Platform Shipboard Gravity Meter," Geophysics 32, 1 (1967).

[2] W. A. Prothero and J. M. Goodkind, "A Superconducting Gravimeter," Rev. Sci. Instrum. 39, 9 (1968).

[3] J. M. Goodkind, "The Superconducting Gravimeter," Rev. Sci. Instrum. 70, 11 (1999).

[4] N. Courtier et al., "Global Superconducting Gravimeter Observations and the Search for the Translational Modes of the Inner Core," Phy. of the Earth and Planetary Interiors 117, 1 (2000).

[5] I. Marson and J. E. Faller, "g - the Acceleration of Gravity: Its Measurement and Its Importance," J. Phys. E: Sci. Instrum. 19, 22 (1986).

[6] W. Demtröder, Laser Spectroscopy, 3rd (Springer, 2003).

[7] M. A. Kasevich and S. Chu, Phy. Rev. Lett. 67, 181 (1991).

[8] J. B. Fixler, G. T. Foster, J. M. McGuirk and M. A. Kasevich, "Atom Interferometer Measurement of the Newtonian Constant of Gravity," Science 315, 74 (2007).