3:2 Mercury-Sun Synchronization

Introduction

Why does the Moon always show the same face to us, even though it is constantly orbiting around the Earth? The fact that the Moon rotates on its axis with exactly the same frequency with which it revolves around the Earth might strike many as a surprising coincidence, but in fact, such synchronous motion is not an unusual phenomenon in our solar system. All the other planets in the solar system have been discovered to have most of their moons rotating in the same synchronized way the Moon does with the Earth. Such synchronization between a planet and its moons is mainly due to the "tidal locking process," which I will explain.

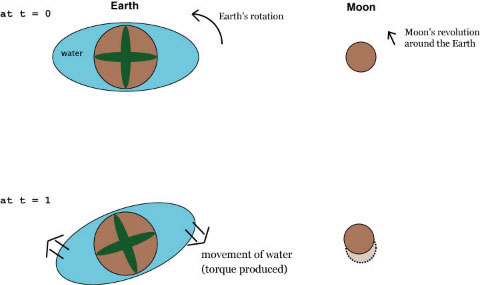
Fig. 1: The rotation of the Earth slows down due to the friction from the tides which is governed by the Moon.

However, there is one exceptional case of a synchronized motion in our solar system which cannot not be explained by the tidal locking process. When a body is tidally locked to its neighbor, it rotates exactly once as it finishes its orbit around its master. Mercury, on the other hand, exhibits a 3:2 synchronization with the Sun. It rotates on its axis one and a half times during the time it completes one revolution. In this report, I will briefly go over the most important studies that have been made that helped explain this peculiar behavior of Mercury.

Tidal Locking

Before I start on the motion of Mercury, I will first explain how the tidal locking works, using a nice example of the Earth which is in the process of tidal locking onto the Moon at the moment. Figure 1 qualitatively illustrates how the tides on the Earth produces torque against the Earth's rotation. Two bulges of water on each side of the Earth, which is drastically exaggerated in the figure, are always aligned with the line which connects the Moon and the Earth. But since the Earth is rotating much faster (frequency: 1 day) than the rotation of the bulges (frequency: 1 month), a friction is generated between the water and the Earth. This works as a brake that slows down the rotation of the Earth. It is easy to see that this process will continue until the rotation of the Earth becomes much slower and synchronizes with the revolution of the Moon.

Fig. 2: The Moon gains energy from the biased gravitational pull from the tides on the Earth.

Decrease in the Earth's rotational speed due to the tidal locking is not easy to measure directly, but it is one of the many factors that contributes to the occasional addition of one "leap second" to our standard times. Because the Earth is slowing down, a day is getting contantly longer every year, while the standard time is defined by a fixed number of ticks in the atomic clocks. In order to compensate the discrepancy between the two, a second is added to our clocks every now and then, and this is called "a leap second." As of now, year 2007, the last leap second which has been added to our time occurred at the transition between the year 2005 and the year 2006.

Just to complete the story, there is also the conservation of angular momentum which affects the Moon as well. If the Earth is rotating ever more slowly and losing its angular momentum, where does this missing angular momentum go? It turns out that the Moon picks up this angular momentum and revolves around the Earth with increased energy. This is illustrated in Fig. 2. Although the two separate cartoons might give a false impression that these two processes are independent of each other, they are actually a direct consequence of Newton's action-reaction law, and thus the lost rotational angular momentum of the Earth is compansated by the gain of the Moon's orbital angular momentum.

After gaining more energy and the angular momentum, the Moon will move farther away from the Earth, the process of which is not clear from the picture. To see how this works, let's assume that the Moon's orbit around the Earth is perfectly circular. The Kepler's third law says that

where a is the radius of the orbit, and P is the period of the planet which can be rewritten as

Here, v is the speed of the planet. Combining these two equations gives us

Because the angular momentum of the orbiting planet is given by

we can see that the increase in the angular momentum leads to a smaller v and a larger a. Increasing distance between the Moon and the Earth has been recorded quite accurately using the laser pulse bouncing experiment: 3.84±0.07 meters per century.[1]

Mercury

Fig. 3: Synchronized one and a half rotation of Mercury as it orbits around the Sun

In 1965, the rotational period of Mercury was measured for the first time using the radar Doppler-spread [2]. Until then, it was generally believed that Mercury was synchronously tidally locked to the Sun, as the Moon has done to the Earth. Therefore, when the result of the experiment was published that the measured rotational period was 59±5 days, significantly shorter than the orbital period of Mercury (88 days), this immediately drew many physicists' attention.

Colombo [3] was the first to point out that Mercury's rotational period might actually be exactly two third of the orbital period, thus in sync with its revolution, only not by 1:1 but with 3:2 ratio. Mercury has the largest orbital eccentricity (e = 0.2056) among all the Solar planets (besides Pluto, e = 0.2482, which has been recently demoted to dwarf-planet status). Colombo claimed that since the distance between Mercury and the Sun varies significantly, the motion of Mercury must be regulated by the gravitational effect most heavily at perihelion. As shown in Figure 3, the only way to enforce a stabilized orientation of Mercury at its perihelion is to let it have the rotational period a multiple times of a half of the orbital period. Colombo also pointed out that the orbital angular velocity of Mercury at perihelion is

leading to approximately 1:1 synchronization near perihelion if Mercury is 3:2 synchronized.

The key to understand the peculiar behavior of Mercury is to look at it as a rigid system that has no fluid or gas on its surface. Because it is rigid, there is no tidal effect that can generate friction. It is only the asymmetry of its shape that provides a handle for the Sun to control its rotation.

Liu and O'Keefe [4] used MacCullagh's formula for the potential energy of a planet

to run a numerical simulation of the Mercury's motion. Here, K is the gravitational parameter, M is the mass of Mercury, I is the moment of inertia around the radius vector r, and A, B, C are the principal moments of inertia. They found, even for a small distortion in the spherical shape of Mercury,

Mercury locks into 3:2 synchronization, given the eccentricity e = 0.2. This was the first calculation that showed that locking in fractional ratio is actually possible.

Later, as more accurate measurements on Mercury's rotation were made using high resolution images sent from Mariner 10, NASA's first Mercury probe, it was confirmed that Mercury is indeed rotating around the Sun at 3:2 resonance. NASA's second Mercury-bound spacecraft, MESSENGER, has been launched in 2004, and is scheduled to fly by Mercury in January 2008.

References

[1] G. O. Dickey et al., Science 265, 482, (1994).

[2] G. H. Pettingill and R. B. Dye, Nature 206, 1240 (1965).

[3] G. Colombo, Nature, 575 (1965).

[4] H. S. Liu, and J. A. O'Keefe, Nature 24, 1717 (1965).