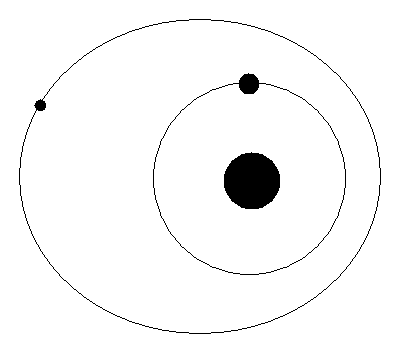
 |
| Fig. 1: Illustration of orbit period commeasurability. Click to start or stop animation. |
In the solar system, there are a large number of orbit sets (two or more) whose frequencies or periods have simple numerical relationship between them. In the expression of mean motion
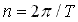
that is to say
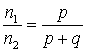
where p and q are both small integers. This is not a simple coincidence but an important gravitational effect called orbital resonance that determines the dynamical structure of the solar system. In the orbits with simple numerical relationship, the objects have periodic gravitational influence on each other (Fig. 1). These influences usually lead the system to a stable resonant structure; if the objects do not collide with other asteroids.
A famous example of orbital resonance is the Laplace resonance between Jupiter's three satellites Io, Europa and Ganymede. Their mean motions have relation
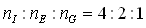
However, in the case of Saturn's rings, the ring dusts in 2:1 resonance with Mimas are actually cleared out by increased collisions, therefore form the gap between the inner and outer rings.
Laplace is the first one who studied this subject. Very comprehensive and detailed theories have been analyzed since then. This report is aiming at describing the physics in this phenomenon without reaching the analytical details.
Consider two objects m and m' ( m >> m') with commeasurable orbit periods orbiting around the primary mass M (Fig. 2). Thus the gravitational influence from m' on m is negligible. Assume the eccentricity of the inner orbit is very small, e.g. the orbit is almost a circle, and the outer orbit is slightly elliptical. The two objects are called to be at conjunction when their longitudes are the same since they are closest to and thus have most influence on each other then. If the conjunction happens at the apocenter or pericenter of the outer orbit, the tangential forces acting on m' are symmetrical before and after the conjunction. Therefore the angular momentum of m' will not change after conjunction.
For the outer orbit with large eccentricity, when the conjunction does not happen at the apocenter, consider it happening before apocenter as shown in Fig. 2. Because their orbits are diverging around conjunction, the tangential force m' experiences before conjunction is larger than it experiences after conjunction. Meanwhile the relative angular velocity of the objects is larger after conjunction. Thus the time that m' experiences disturbing force from m is longer before the conjunction. Therefore m' losses angular momentum and thus decreases in period after the conjunction. Then m will spend more time to catch up with m' next time since the mean motion of m' becomes faster, which means the conjunction will happen later and thus closer to the apocenter. With similar analysis of conjunction happening at other places, it is clear than all the conjunctions tend to move towards the apocenter under the influence of m on m'.
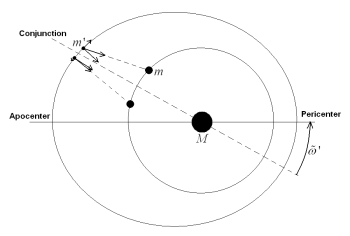 |
| Fig. 2: Schematic illustration of two objects in periodic conjunction. The inner orbit has negligible eccentricity. The object on the outer orbit has negligible mass. |
However, after the two objects adjust their orbits to the most stable conjunction place, they do not really stay there. The inner orbit will be expanded over time due to the tidal interaction between m and the primary mass M. This decreases the angular momentum of m and thus causes the conjunction to happen after the apocenter. And then the mechanism discussed above will adjust the conjunction back to the apocenter.
There are also two effects of the radial force to be considered. First, every time when the two objects are in conjunction at apocenter, m' experiences an impulse radial force from m, which drags m' more into the inner space. That actually brings forward the pericenter of m'. Thus the m' orbit rotates in a retrograde way, which dominate the orbit rotation when m' is sufficiently small.
Second, since the tidal interaction between m and M always postpones the conjunction, m' experiences impulse radial force after the apocenter and falls closer to the primary mass, which increases the eccentricity. These effects actually provide a second resonance mechanism.
For the outer orbit with small eccentricity, the angular momentum transfer mechanism discussed above is largely weakened. Instead the line of apsides is more easily changed due to the impulse radial force. Hence we need a more useful criterion of resonant situation to find the periodic influence:
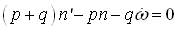
This equation means the two orbits are commeasurable in a frame rotating with the line of apsides.
As discussed above, the impulse radial force near apocenter causes the orbit of m' and thus the conjunction to rotate in a retrograde way. Also as discussed above, the impulse radial force applied after apocenter increases the eccentricity. That weakens the effect of the apocenter's retrograde rotation due to the falling in of m'. As a result the apocenter is caught up a little by the conjunction which originally rotates with the apocenter. Similarly, if the conjunction happens before apocenter, the impulse radial force will cause the apocenter to catch up with the conjunction a little. Therefore the apocenter librates around the conjunction.
Different from the large eccentricity case, conjunction at the pericenter could also build up a resonance in m' orbit of small eccentricity. The analysis is exactly conjugate with that for conjunction at pericenter.
© 2007 Y. Jiang. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] C. D. Murray and S. F. Dermott, Solar System Dynamics (Cambridge, 1999).
[2] S. J. Peale, "Orbital Resonances in the Solar System," Ann. Rev. Astro. Astrophys. 14, 215 (1976).