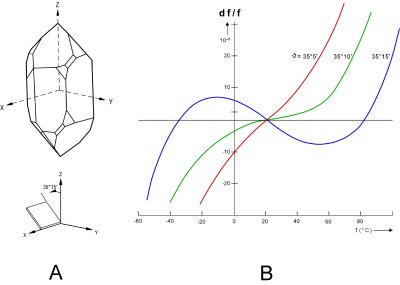
 |
| Fig. 1: A) Illustration of AT-cut quartz crystal. [5] B) Frequency shift as a function of temperature for different cut angles. [5,8] |
Upon application of an electric potential, certain crystals will deform physically, and vice versa; this property is known as piezoelectricity. Since mechanical stress cannot separate electrical charges, piezoelectricity is caused by the physical or electric-field induced alteration of pre-existing permanent dipole moments, arranged without a center of symmetry in a crystalline unit cell. [1] Out of the 32 crystal classes, based on symmetry arguments alone 20 are potentially piezoelectric, but the magnitude of the piezoelectric response in a given crystal depends on specific details. [2] The mechanical strain and applied field can be related by the matrix equation x=d*E, where d is the piezoelectric strain coefficient matrix. In quartz, five of the 18 elements of the d matrix are zero, and only two are independent. [3]
The main utilities of piezoelectricity are (1) the coupling of an electrical signal with the mechanical world, which has significant applications in sensing and actuation; and (2) the fabrication of high-fidelity oscillators and frequency standards. Quartz is the most commonly used crystal used in both applications, due to its strong piezoelectric response, abundance, processability, and anisotropy. [4] The last is important in that different cuts of quartz have different responses to temperature and stress. Elastic constants too have temperature dependence. By using this to advantage, quartz can be cut in such a way as to have very low frequency shift as a function of temperature near room temperature; these are "temperature compensated" crystals (Fig. 1). [3]
Due to charge leakage, application of a steady force produces only a transient voltage which can be as high as 20kV. [5] Thus piezoelectricity is essentially always used subject to an AC field, with the added advantage that frequency is currently one of the most precisely measurable quantities. The oscillations induced under application of AC field can either be bulk modes or surface acoustic (Rayleigh) waves, depending on the application and on the desired frequency. [6]
Bulk acoustic wave resonators cover the frequency range of about 1 kHz to 500 MHz depending on cut and vibration mode. The most commonly used especially in mass sensing applications is an AT-cut crystal in a rectangular or circular plate with electrodes of similar geometry, vibrating in a thickness-shear mode, which has the added benefit of limiting energy loss to a fluid medium (Fig. 2). [7] This mode is, in an idealized picture, approximately equivalent to a transverse wave traveling in the thickness direction of the plate. In the case of a rectangular plate the equation of motion is therefore
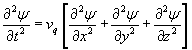
where the displacement ψ is perpendicular to the direction of propagation and vq is the wave velocity which depends on the density and applicable elastic constants. Assuming that the plate is not clamped, the center of the plate is a node, and this provides the necessary boundary conditions for a solution
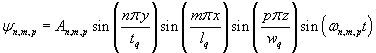
where n, m, and p are odd counting indices and tq, lq, and wq are the thickness, length and with of the plate. [3] The frequencies are
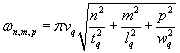 .
.
These are just standing waves in the x, y, and z directions. If lq and wq are very large compared with the thickness
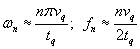 .
.
In the limit of large radius to thickness ratio this same result is obtained in the case of the circular plate, and coupling with contour modes at the plate edges can be neglected. [2,3] At a typical drive current at this resonant frequency, the maximum displacement is on the order of a few atomic spacings. [4]
One very common use of the quartz crystal resonator described above is as a mass sensor, often in determination of thin-layer thickness or in gas sorption studies. [5] It can also be used as a chemical sensor if the surface of the microbalance is pre-covered in a chemically sensitive layer.
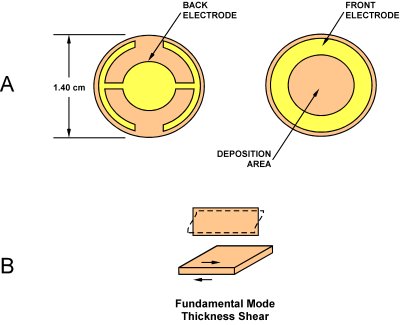 |
| Fig. 2: A) Schematic of typical quartz crystal microbalance. [10] B) Illustration of transverse shear mode of oscillation. [4] |
An explicit quantitative relationship between shift of resonant frequency and added mass, is important to ease of use in a quartz crystal microbalance (QCM). This relation was first derived by Sauerbrey in 1959. [8] As mentioned earlier, the fundamental resonant frequency of the quartz crystal bulk thickness-shear mode is vq/2tq. Differentiating this to obtain the resonant frequency shift caused by an infinitesimally small change of crystal thickness gives
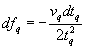 .
.
The relative change of frequency is therefore
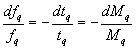
where Mq refers to the crystal mass and dMq the incremental change in mass of the quartz crystal. If the approximation is made that the increment of foreign mass dMf is approximately equal to dMq, then the relative change of resonant frequency upon film deposition is
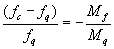 .
.
fc is the resonant frequency of the combined quartz plus foreign layer. This can be rewritten per unit area by dividing the numerator and denominator on the right by area. Letting m refer to the mass per unit area, and assuming both the quartz and the foreign layer have uniform densities ρq and ρ f respectively, we have
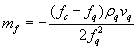 .
.
This is the required relation between the foreign added mass and the change in resonant frequency. [5] It is typical to define a crystal calibration constant Cf that is
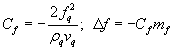 .
.
In practicality other factors like damping in the electrical circuit, mechanical clamping, and temperature do affect the accuracy of the above approximation, and it is therefore most common to use calibration curves for routine quantitative work. Nevertheless the QCM is a very sensitive and stable sensor. In a typical example, the density is 2650 kg m-3 and the shear velocity (AT-cut) is 3340 m s-1. With a resonant frequency at 5 MHz, the crystal calibration constant is 5.65 MHz cm2 kg-1 which implies that a 17.7 ng cm-2 added weight is sufficient to shift the resonant frequency by an easily-detectable 1Hz. The dynamic range of the QCM extends to about 20 μg/cm2 but the Sauerbrey equation is not accurate in the high-mass-density regime. [5]
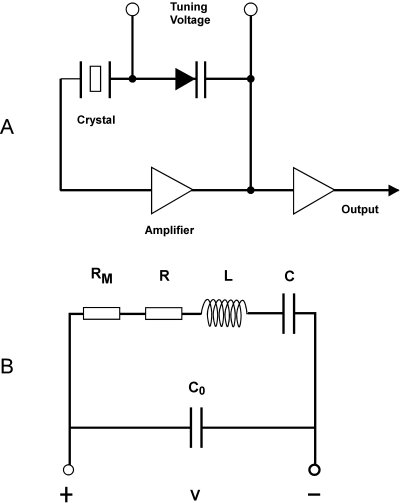 |
| Fig. 3: A) Simplified oscillating driving circuit schematic for a quartz crystal. [4] B) Circuit equivalent diagram for a quartz crystal. [11] |
As a damped, driven harmonic oscillator, the QCM can be modeled as an electrical circuit, as indicated in Fig. 3. Mechanical elasticity is modeled by motional capacitance C, vibrating mass by electrical inductance L, and energy loss by electrical resistance R. [9] In this model an increase in system mass will be observed as an increase in the value of L, C, and mechanical load RM, and hence a decrease in the resonant frequency. [5] However, an explicit quantitatively correct value for the frequency shift as a function of absolute added mass is not easy to obtain using a circuit equivalent and so the relation obtained in the previous section is still important.
In a practical example, the value of C in a typical 5MHz AT-cut quartz crystal is on the order of 0.01 pF, L is on the order of 0.1H, and R is on the order of 10 ohms. Collectively this set of values would be very difficult to obtain using inductors and capacitors. [3] Equivalently the Q-factor of a quartz crystal unit is on the order of 104-10 [6], compared with typical values of several hundred for ωL/R in an equivalent electrical circuit. The maximum attainable Q*f (f in MHz) is approximately 16 million [4] although for microbalance applications the less controlled packaging makes this somewhat lower. [7]
The resonant frequency of the quartz crystal resonator in equivalent circuit terms is
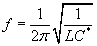
where C* is simply C when a capacitive load is connected in series with the unit (fs), but C0C/(C0+C) when the capacitive load is connected in parallel (fp). [3] The quartz crystal is typically driven in a oscillator circuit, in which the crystal is part of a positive feedback loop requiring a total phase shift of n2π around the loop for stable oscillation. [4] Often parallel capacitances are compensated in such circuits and the crystal is driven as nearly as possible to its series resonant frequency. [7]
For the QCM, typically users are concerned with measuring mass changes, and thus frequency shifts, that take place on the order of minutes to hours, as in those that result from thin film deposition or chemical reaction. Thus many of the causes of long-term frequency drift in quartz crystal resonators (surface or electrode reaction or deterioration, mechanical stress due to mount and electrodes, radiation-induced defects, etc.) [3] which are important in the use of quartz crystals as frequency standards, are of less concern in these applications. Environmental effects such as changes in frequency with drive amplitude or with orientation relative to the Earth's gravitational field are also of limited concern, since they can be typically held constant for a single QCM experiment. [3] However, temperature fluctuations could cause thermal frequency shifts to become problematic, especially if the experiment is not being done near room temperature.
The most usual inaccuracies for microbalance applications are caused by limitations in the validity of the approximate linear relationship between mass and frequency shift. Sauerbrey's relation breaks down as mf << mq ceases to be valid. For larger mass densities more complex expressions relating the added mass to the resonant frequency have been derived using a model of a composite (two-layer) resonator, but these too make approximations. [10] Also while Sauerbrey's relation is generally valid for mass measurements in fluids, the fluid represents an additional dissipative load, through coupling of the elastic shear wave to the fluid. The magnitude of this coupling depends significantly on interface chemistry; it can be greatly impacted by even monolayers of added foreign mass. The resulting frequency shift is not related to the magnitude of the added mass and often precludes QCM techniques entirely. [5]
© 2007 S.L. Hellstrom. The author grants permission to copy, distribute and display this work in unaltered form, with attributation to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] A. von Hippel, Z. Physik 133, 158 (1952).
[2] L.E. Halliburton, J.J. Martin, and D.R. Koehler, in Precision Frequency Control Volume 1: Acoustic Resonators and Filters, ed. by E.A. Gerber and A. Ballato (Academic Press, 1985).
[3] V.E. Bottom, Introduction to Quartz Crystal Unit Design (Van Nostrand Reinhold, 1982).
[4] J.R. Vig, Army Research and Development Technical Report No. SLCET-TR-92-1 (Rev. 1), 1992.
[5] J. Janata, Principles of Chemical Sensors (Plenum, 1989).
[6] W.L. Smith and T.E. Parker, in Precision Frequency Control Volume 2: Oscillators and Standards, ed. by E.A. Gerber and A. Ballato (Academic Press, 1985).
[7] R. Lucklum and F. Eichelbaum, Springer Ser. Chem. Sens. Biosens. 5, 3 (2007).
[8] G. Sauerbrey, Z. Physik 155, 206 (1959).
[9] F. Eichelbaum et al., Rev. Sci. Instrum. 70, 5 (1999).
[10] C.-S. Lu and O. Lewis, J. Appl. Phys. 43, 4385 (1972).
[11] M.A. Tenan and D.M. Soares, Br. J. Phys. 28, 405 (1998).