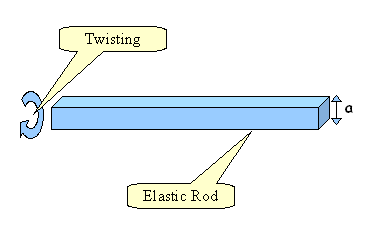
Then the bending energy can be written as
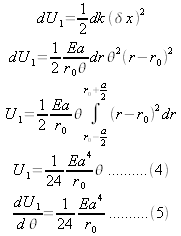
If a buckling happens after enough twisting, the
energy required to form a circular writhe with a radius r0
:
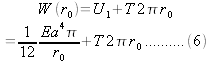
This energy cost is minimum at a certain radius. It
is well-known that the geometric mean of the numbers is always less then
the arithmetic mean of them. Therefore,
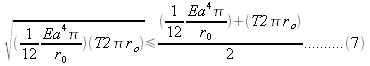
Then the minimum required energy:
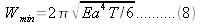
And the radius:
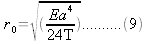
The torsional energy of a twisted elastic rod is
U2(φ)=½κ φ2, where
φ=2nπ the twisted angle and κ is the torsional
coefficient.
At the critical torque value, the work done by
twisting the rod by one rotation, must be equal to the conformation
energy of the loop.
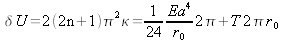
So the twist number required for buckling a writhe:
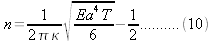
This simple model explains how the two types of
coiling of DNA related with each other.
© 2007 U. Eser. The author grants permission to
copy, distribute and display this work in unaltered form, with
attribution to the author, for noncommercial purposes only. All other
rights, including commercial rights, are reserved to the author.
References
T. Strick, "Twisting and Stretching Single DNA
Molecules," Prog. Biophys. Mol. Bio. 74 , 115 (2000).
J. H. White, "Self Linking and the Gauss Integral in
Higher Dimensions," Am. J. Math. 91, 693 (1969).