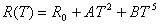
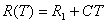
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Table 1: Values of R0, A, B, R1, and C for selected metals. [2-5,7] |
The resistivity of a crystalline solid, R(T)=e/J (where e is the applied uniform electric field and J is the resulting current density), in the case of many metals exhibits predictable behavoir at low and high temperatures. In the low temperature limit, R(T) often follows some combination of a second and fifth order power law with temperature. Where the former is generally from conduction electrons scattering off spin-waves in a stationary magnetic lattice or scattering between s and d orbital electrons and the latter is from scattering off of phonons. In the high temperature limit, the resistivity of metals almost universally exhibits the familiar linear dependance on temperature.
At low Temperatures: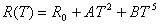 |
At high Temperatures: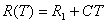 |
The Boltzmann Equation for a collisions process is [5]: df/dt|fields + df/dt|collisions=0, where f is the charge carrier distribution. In the presence of an electric field, to first order: df/dt|fields= dE/dt|fields df0/dE = -vqe df0/dE (here f0 is the equilbrium Fermi-Dirac distribution, v is the charge carrier velocity, and q its charge). We assume that any charge carrier is equally likely to collide at any point in time: df/dt|collisions= -(f-f0)/trelax (trelax is the familiar relaxtion time from the Drude model). We thus have:
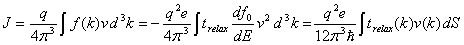
with the S being the Fermi surface. In the special case where trelax is independant of k and v is the Fermi veleocity we recover the Drude resistivity R=m/(nq2trelax), with m and n being the mass and number (at the Fermi surface) of the charge carriers respectively.
The usual tool for calculating trelax is to simply solve the collision problem:
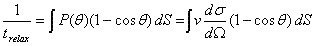
In the case of electrons in a metal scattering off of impurities, the collision cross-section is constant and the conduction electrons travel at the Fermi velocity [1,5]. This gives the important result that there is a constant (non Temperature-dependant) component of the resistivity corresponding to impurities embedded in a metal.
In many materials, Electron-Phonon scattering is the dominatant source of the temperature-dependant resistivity. The temperature-dependant cross-section for phonon scattering only depends on the scattering matrix element, Vkk'2 [1,5].
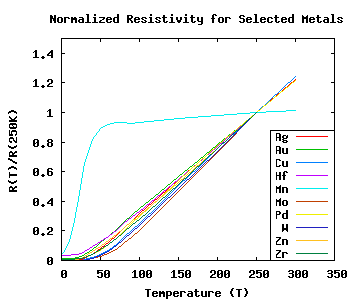 |
| Fig. 1: Dimensionless Behavoir of Resistivities with Temperature [2-4,7]. |
At high (above the characteristic speed of sound-based Debye Temperature) temperatures, classical equipartition (E=kt/2 per oscillator degree of freedom) gives that the scattering matrix element, which is proportional to the oscillator energy, is simply linear in temperature. For metals, and many other materials, the Drude resistivity is valid and the only temperature dependant part is 1/trelax, which we have just shown is linear in T. We have thus derived that at high temperatures electron-phonon scattering, which turns out to be the dominant contribution to the resistivity, causes the familiar linear temperature dependance.
At low temperatures, the phonon frequency (and hence the momentum) will be proportional to the temperature, so these low-momentum scattering events will deflect the electrons at small angles (We assume low temperature scatters have a reciprocal lattice vector, G=0; scatters where G is nonzero, affectionately referred to as Umklapp events, will in general have a much steeper, less predictable, temperature-dependance.). The Vkk'2 are linear in phonon momentum and the Fermi surface area (or rather, number of phonons on the Fermi surface) grows as T2. We thus have that:
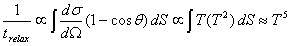
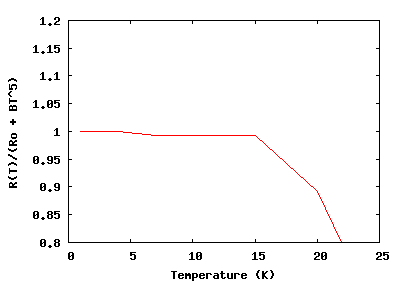 |
| Fig. 2: Plot of R(T)/(R0 + BT5) for Zinc showing quintic temperature dependence of the resistivity. [3] |
In many magnetic solids, the aligned (or anti-aligned) electron spins precess slightly about their ground states, which are in otherwise fixed positions. These are small variations about a potential minima so are thus harmonic oscillators obeying Bose-Einstein statistics, much like phonons, and are called spin-waves or magnons. However, due to the way spin-waves pack, we have ω ∝ qm2, where qm is the wave-number [1,5].
Now, the cross section for a conduction electron scattering off a magnon (the conduction electron spin simply flips) is independent of the magnon momentum. Thus, as with phonon scattering, the scattering angle is proportional to q and the Fermi surface is populated by qm2 magnons. It directly follows that:
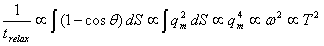
That is, magnon scattering causes a T2 dependance in the low-temperature resistivity.
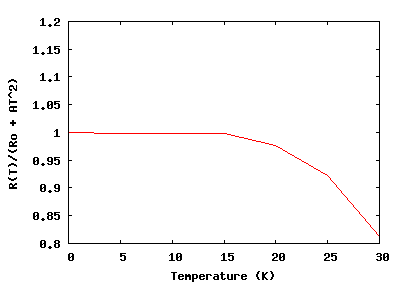 |
| Fig. 3: Plot of R(T)/(R0 + AT2) for Manganese showing quadratic temperature dependence of the resistivity. [2] |
In other metals, the d-orbital electrons, with are delocalized, are those causing the magnetism. Very roughly speaking, the conduction (also the d-orbital) electrons can only gain or lose Energy kT from colliding with an s-orbital electron. This means that both an occupied and an unoccupied slot must exist in the d-orbital within the energy band of kT from the Fermi level. For low temperatures, the probability of finding such states is proportional to T for both. So the probability for such a scattering event is proportional to their product, T2. In this case then, we have:
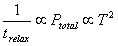
This type of scattering, too, causes a T2 dependance in the low-temperature resistivity.
The data used can be downloaded here. Plots were built using gnuplot.
© 2007 Kipp A. Rogers. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] R. G. Chambers, Electrons in Metals and Semiconductors (Chapman and Hall, 1990).
[2] C. Desai, H. James and C. Ho, "Electrical Resistivity of Aluminum and Manganese," J. Phys. Chem. Ref. Data. 13, 1131 (1984).
[3] ibid., "Electrical Resistivity of Selected Elements," J. Phys. Chem. Ref. Data 13,1069 (1984).
[4] ibid., "Electrical Resistivity of Vanadium and Zirconium," J. Phys. Chem. Ref. Data 13,1097 (1984).
[5] J. S. Dugdale, The Electrical Properties of Metals and Alloys (Robert E. Krieger, 1979).
[6] W. Leonard and T. Martin, Electronic Structure and Transport Properties of Crystals (Edward Arnold, 1977).
[7] R. A. Matula, "Electrical Resistivity of Copper, Gold, Palladium, and Silver" J. Phys. Chem. Ref. Data 8, 1149 (1979).