After Roentgen discovered the X-ray in 1895, Laue developed the diffraction theory in 1910, and his assistants Friedrich and Knipping used X-ray to observe the diffraction pattern of salt to prove that crystals have lattice structures in 1911. X-ray crystallography has since become a popular method to determine the structure of crystals. Today, the X-ray crystallography is widely used by pharmaceutical companies to resolve the interaction between drugs and their proteins targets. Around 36000 protein structures in the protein data bank (PDB) are the results of X-ray crystallography [2]
|
|
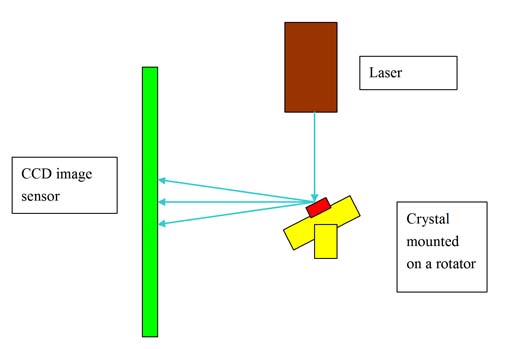
| Fig. 1: A typical X-ray crystallography setup. |
To do a crystallography experiment, one needs a crystal sample, an X-ray source and an X-ray detector to record the reflection of the X-rays. The sample crystal is mounted on a rotator in order for the X-ray to illuminate the sample at different angles. The crystal reflects the X-rays, and the reflected signal is then recorded by the X-ray detector. The experimental setup is described in Fig. 1.
The sample crystals must be very pure in composition, have no cracks, and be large enough to give a strong signal. Since the distance between two atoms in a crystal need to be determined to within tenths of an angstrom (A), the radiation chosen also needs to have a wavelength short enough to achieve desirable resolution. Bragg's law says that
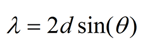
where lambda is the wavelength, d is the distance between two lattice planes, and theta is the angle of incidence. The maximum allowable wavelength is thus 2d. X-rays are chosen as the radiation source since the wavelengths of X-rays are between 10-7 and 10-11 meter (1000 - 0.1 Å). Shorter wavelength X-rays are not desirable. While X-rays with shorter wavelengths have lower chances of destroying the sample because of their lower absorption cross section, the disadvantage is that they also produce weaker diffraction signals. The optimum wavelength for protein crystallography is 1.5418A generated by a Cu K-α X-ray.
 |
| Fig. 2: Geometry of incident and diffracted radiation. The wave vectors kout and kin are parallel to the propagation of the wave. We also have |kout|=|kin|, and q = kout - kin. For every point on the detector, there are a corresponding q and I(q). |
The common monochromatic X-ray sources are the synchrotron and the sealed X-ray tube. The synchnotron produces X-rays at high luminosity and with tunable wavelength. However, synchrotrons mainly exist in large national labs while sealed X-ray tubes, which are smaller and less expensive, are available in normal labs. Therefore, the later are used primarily by X-ray crystallographers for preliminary qualitative work.
Historically, the intensities of the reflections of the X-rays were first recorded by photon counters. Subsequently, X-ray setups evolved to use photographic films, area detectors, and, eventually, charge-coupled device (CCD) image sensors.
X-ray crystallography works by mapping the electron density f(r) of the molecule by taking advantage of diffraction theory and the Fourier method. Diffraction theory models the incident X-ray as a plane wave with a wave vector kin and frequency ω. At the position r in the crystal, the wave has the amplitude A and phase kinr
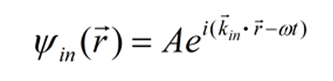
The frequency ω is a constant throughout the scattering process and will be omitted from now on. [1] After scattering by electrons in a small volume dr containing the electron density f(r), the amplitude of the wave arriving at the screen is proportional to both the electron density and amplitude of the incident wave, per
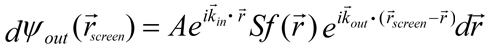
where S is just a proportionality constant. [1] The total scattered wave is thus
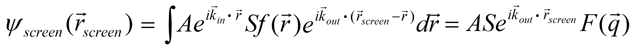
where q equals kout - kin. Since the scattering is elastic (no energy is lost) we have |kin| = |kout|. The measured intensity I is proportional to the square of the amplitude.
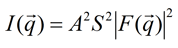
Unfortunately, F(q), the Fourier transform of f(r), and is a complex function with a magnitude part |F(q)| and a phase φ:
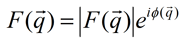
While one can directly obtain the magnitudes |F(q)|, the phases φ(q) are more difficult. They may be (1) guessed, (2) inferred by alternating the wavelength of the X-ray across the absorption edge of the crystal or (3) inferred from changes that result from adding heavy atoms such as mercury to the sample. Once the phases and the magnitudes are obtained and assembled together, F(q) can be inverted to obtain the electron density map f(r).
Before diffraction theory and the Fourier method were introduced to X-ray crystallography, the data analysis was a process of trial and error. Crystallographers assumed a possible crystal structure and the X-ray diffraction pattern it would create. If the pattern and the experimental result didn't match, then they would guess another possible structure, and so on. Later, the law for intensity of diffraction helped to quantify the results of calculations and experiments. Knowledge of the sizes, the numbers, and the kinds of atoms based on X-ray spectrometry, and the likely chemical grouping of the atoms also aided the guessing. The Fourier method made the guessing even easier because it directly related the intensity of diffraction to the amplitudes |F(q)|. However, since the phases φ(q) were unknown, guessing was still inevitable.
The phases were guessed based on the criterion that the results must be physically sensible. For example, after inverse Fourier transforming F(q) back to electron density f(r), f(r) must give the right number of atoms, the right electron distribution, and the density must be positive everywhere. Phase guessing based on reality was called the direct method.
Several methods are used today to guess the "initial phases" for macromolecules: molecular replacement, anomalous scattering, heavy atom methods, and ab initio phasing. Molecular replacement requires a known crystal structure of a related molecule, or a known crystal structure of our sample in a different crystal form. The known crystal structure works as a search model to settle on the position and orientation of the unit cell of the sample.
The anomalous scattering method involves X-rays of at least three different wavelengths, far below, far above, and in the middle of the absorption edge of some atoms. Because the absorption cross section increases (thus scattering cross section decreases) significantly over the absorption edge of those atoms, the positions of those atoms can thus be solved. Then various techniques can help to resolve the relative positions of other atoms to those atoms.
Crystallographers also use the "heavy atom" method that involves adding one or several heavy atoms into a unit cell. The position of the heavy atoms is usually easy to obtain [3].
Ab Initio phasing is based on the direct method. It works only when the number of atoms in a unit cell is fairly few (<500) and high resolution data exist.
After guessing the initial phases, crystallographers can build an initial model. They can then refine phases from the initial model, which leads to a better model, and so on. The process contiues until the correlation between the model and the diffraction data is maximized. The correlation is gauged using various factors such as R-factor, and Rfree, etc.
Many free resources are available on line to analyze the X-ray diffraction of macromolecules such as proteins. The programs incorporate different functions: crystal characterization, initial phases guessing, phase refining, and graphing. Programs like HKL2000, etc., can evaluate the data by indexing, integrating, and scaling them. Programs like CNS package and DETWIN in the CCP4 package, etc., can separate two or more copies of reciprocal lattice when they overlap. Multiple copies occur when the crystal has different domains. The protein data bank (PDB) provides the search model of initial phasing for molecule replacement method. Programs like CNS and Amore, etc., can refine the phases. There are also other programs dealing with gradient energy minimization, manually refining the data when water molecules are present, etc. An X-ray crystallography experiment might require more then ten programs to analyze the data [4].
After a series of guessing and refinements, the density map might still not be 100% accurate, especially for macromolecules with a huge unit cell. Some atoms may have too much residual disorder so they become imperceptible. Crystals with other imperfections, such as small sizes or multiple domains, also render the data analysis difficult. Some atoms with small electron density, such as hydrogen, also become unnoticeable. On the other hand, an experiment might predict multiple positions of an atom while in fact only one exists in the unit cell. This happens when the lattice has several allowed conformation.
© 2007 Yun-Chieh Peng. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] Wikipedia contributors, "X-ray crystallography," Wikipedia, The Free Encyclopedia, (accessed June 9, 2007).
[2] PDB Statistics. RCSB Protein Data Bank. Retrieved on 2007-05-03.
[3] L. Bragg, Development of X-ray Analysis (Dover, 1992).
[4] T. Okada et al., "Functional Role of Internal Water Molecules in Rhodopsin Revealed by X-ray Crystallography," Proc. Natl. Acad. Sci. 99, 5982 (2002).