In E&M, we learned the famous formula for dielectric materials: D(r) = ε E(r). D is the electrical displacement, which is related to the electric field caused by the free moving charge (the externally added charge). E is the electric field caused by the total charge, which includes the free moving and the bound charge (the internally induced charge). ε is the dielectric constant, also called permittivity, which relates the D to E. ε is infinite for metals in the limit where the applied field is spatially uniform. In this case, the electrons inside the metal are free to arrange themselves until their own electric field exactly counters the externally applied field D. Thus, the total field E becomes 0.
However, when a spatially and temporally varying field is applied, ε is not infinite even inside a metal. Instead, it varies with positions inside the medium (r), the frequency (ω) and the wave vector (k) of the field inside the medium, temperature, and humidity, etc. Here, we will use quantum mechanics to deduce the dielectric function of a metal in two steps. We will first use the free electron model which treats ions as uniformly distributed charges and assumes electrons are the only source of induced charge. The free electron model generates the Thomas-Fermi dielectric constant and the Lindhard dielectric constant by different approximations. We will add ionic induced charge later, which modifies Thomas-Fermi dielectric constant by adding an ionic term.
 |
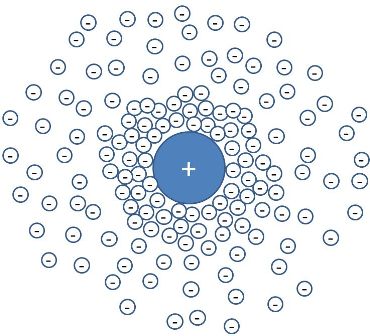
| Fig. 1: Screening of a positive charge inside an electron gas. |
A metal can be considered as an ionic lattice embedded inside an electron sea. The periodic ion lattice causes a periodic potential, which is very hard to calculate. Therefore, we often adopt the free electron model which treats the ions as a uniform background of positive charge even for real metals. This is called a free electron gas.
Screening is an important phenomena in a free electron gas. When an external positive charge density ρext(r) is applied, the electrons will be attracted to surround the positive charge (Fig. 1). The re-arrangement of the electrons generates an induced charge distribution ρind(r). Therefore, the total charge density ρ(r) = ρext(r)+ρind(r) is less positive than ρext(r). Thus, The total potential φ(r) is weaker than the external potential φext(r) caused by the positive charge only. The phenomenon is called screening, which is the primary reason why the electric placement D is not equal to the total field E, and thus ε is not equal to one. By assuming that the applied charge is weak enough so that the total potential and external potential are linearly related, we get the following function in momentum space.
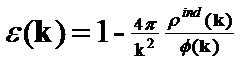
ε is the Fourier transform of the dielectric constant, k is the wave vector of the field, ρind(k) is the Fourier transform of induced charge density, and φ(k) is the Fourier transform of the total potential. The physical consequences of one part of this formula are easy to see. Since one part of ε is proportional to 1/k2, ε is infinite in a spatially uniform applied field where k is equal to zero. The other part of the formula, ρind(k)/φ(k), needs to be solved via the Schrodinger equation with additional approximations. Two commonly used thoeries are the Thomas-Fermi theory of screening and the Lindhard theory of screening.
The Thomas-Fermi theory uses a semi-classical approximation in which φ(r), the total potential, varies very slowly with r. This is equivalent to k being very small. One can then show that ρind(k)/φ(k)=-k02/4π, and thus
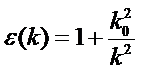
k0 is the Thomas-Fermi wave vector. This formulation takes on a more obvious physical meaning after Fourier transform back to position space, where 1/k0 becomes the characteristic screening length for the exponential decay of the total field inside the metal. For the applied potential of a point charge of Q where φext(r)=Q/r, the total screened field becomes φ(r)=Q/r*exp(-k0/r), which is negligible at distance greater than 1/k0. When T << TF, the Fermi temperature, which is true under everyday conditions for metals,
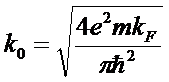
While the Thomas-Fermi theory holds only when k is very small but makes no assumptions about the relationship between ρind(r) and φ(r), the Lindhard theory of screening, also known as Random Phase Approximation (or RPA), takes the complementary approach of making no assumptions about the magnitude of k but instead assuming that ρind(r) and φ(r) are linearly related. Lindhard theory gives the following expression for the dielectric constant.
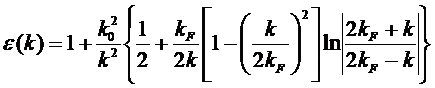
This differs from the simple expression given by the Thomas-Fermi theory by the term inside the {}. With a little math, it can be shown that as k approaches zero, the content inside the {} goes to 1, so that the Lindhard dielectric constant converge to the Thomas-Fermi dielectric constant. However, as k approaches 2 kF, the behavior of ε(k) is no longer analytical. In fact it takes on very complicated behavior thatís beyond the scope of this paper.
So far we have been dealing with a temporally (t) invariant field where the frequency ω of the field is zero. In general, ω could be none zero and ε(k) is actually ε(k, ω=0). In fact, Lindhard theory can give ε(k, ω) as a function of both k and ω. That formula is too complex for the scope of our paper. However, in the spatially (r) homogeneous limit where k=0 but ω not equal to 0, the dielectric constant has an elegant solution:
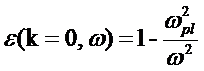
where ωpl2=4πne2/m is the plasma frequency of electrons, n is the electron density, and m is the electron mass. From this formula, we know that when ω = ωpl, ε= 0. In this case, even when no externally applied electric field D is present, the electrons can still collectively oscillate at the plasma frequency.
The free electron model treats ions as a uniform background of charge. However, the assumption fails to notice the fact that ions can also move to screen an external charge. By taking the ions into account,
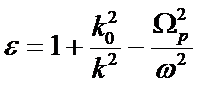
Where Ωpl2=4πni(Ze)2/M is the plasma frequency of ions, ni is the density of ions, Z is the atomic number of the ions, and M is the mass of an ion. The second term on the right side of the formula is a function of k. It comes from the screening of electrons. The third term is a function of ω. It comes from the screening of ions. This formula reveals an interesting point. The importance of the wave vector k relative to the frequency term ω depends on the product of k and the velocity of the charge species. Since electrons move very fast (kv>>ω) , its contribution to ε is k dependent. On the other hadn, since ions move much more slowly than electrons (kv<<ω) , its contribution to ε is actually frequency dependent.
© 2007 Yun-Chieh Peng. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1]P. A. Martin and F. Rothen, Many-Body Problems and Quantum Field Theory, (Springer, 2004).
[2] Ashcroft & Mermin, Solid State Physics (Brooks Cole, 1976).