 |
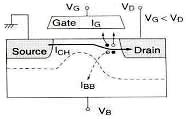
| Fig. 1: Sketch of HCE in a MOSFET [4]. |
Hot carrier effect is of great importance for the MOSFET operation since it is responsible for reliability issues especially in modern short channel devices. On the other hand, this effect is regarded as the programming mechanism in FLASH memory cells, which is a major non-volatile storage device nowadays. The net negative charge in the floating gate stored by injection of "hot carriers" changes the threshold voltage and this change is read as 1 or 0.
Fig. 1 [1] shows qualitative sketch of the hot carrier effect (HCE) in a n-MOSFET. The electrons are, first, accelerated to the critical velocity by the channel electric field (sometimes this is referred as "the carriers are heated", thus, they are called "hot carriers".). These high energy electrons yield impact ionization near the drain and generate hole-electron pairs. The secondary generated holes flow through the substrate (IBB) and cause voltage drop at the body. This voltage drop turns the parasitic BJT on. In the mean time, the hot electrons are injected into the gate oxide - they yield the gate current (IG), but some of them damage the Si-SiO2 interface generating surface sates, or they are trapped in the insulator. If the impact ionization near the drain is too intense, the parasitic BJT behavior would cause large Vth (threshold voltage) lowering, hence rapid increase in ICH and the device failure. We will discuss about how to model this carrier heating phenomenon and hot carrier injection into SiO2 briefly. For modeling of the impact ionization and substrate current, refer [2] and [3].
In order to predict the distribution of hot carriers in a MOSFET, many simplified models have been derived because of the complexity and difficulty of solving the Boltzmann Transport Equation (BTE) directly. These simplified models mostly originates from the BTE, which is given by
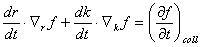
where dr/dt is the electron group velocity and dk/dt is related to the electric field F by the classical Newtonian equation[1].
As the first step to build the simplified model for carrier heating, the simplest equation for calculating average kinetic energy (ω) is suggested from [2,3], ignoring generation-recombination and heat fluxes:

where ω0 = 3 q F(x) / 5, λ0 = 5 νd τE / 3, vd is the drift velocity and τE is the energy relaxation time. The energy relaxation length, &lambda:0, is a function of energy, but in practice it is adjusted to fit the experiment data, which is typically ~65-80nm for electrons and ~ 55-100nm for holes.
By integrating Eq.(2) along the current path, Δω(x) = ω(x) - ω1 can be solved as [1]:
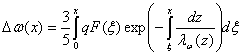
where ω(0) = ω0 = 3 kB TL/2.
The second step of modeling "carrier heating" is to relate this calculated average energy with the shape of the distribution function. In [5] and [6], a simple and improved expression for the carrier distribution was suggested:
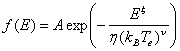
where Te can be approximately derived from the above Eq. (3) such that ω ≈ 3 kB Te / 2.
The parameters (ξ η, ν, λ0) that are used in these models are adjusted to fit the experiment data. These models have been used in the simulations of MOSFETs and Flash cells. However, for small devices (<100nm), more complicated models are required due to the non-local effects.The electron current density from Si to SiO2 can be in general given as [1]:
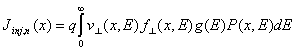
where f⊥(x,E) is the hemi-distribution of electrons that reach the interface, P(x,E) is the injection probability, and ν⊥(x,E) is the electron velocity component that is directed to SiO2. The Eq. (5) is composed of i) (f⊥⋅g), ii) the velocity towards SiO2, iii) the electron energy and momentum distribution ,and iv) the probability of injection from Si to SiO2 (P(x,E)).
The electron energy and momentum distribution may have quasi equilibrium Maxwell-Boltzmann (or Fermi-Dirac) function in which the number of electrons decreases very rapidly as the energy increases. In this case, the injection from Si to SiO2 can occur around at the bottom of conduction band, which means just "pure tunneling" different from hot carrier injection. When VDS > 0 and VGS is large, this can takes place near the source.
 |
| Fig. 2: Gate current vs. VG, HH=hot holes, HE=hot electrons. [7] |
On the other hand, if the tail of the distribution is populated largely, the injection mainly occurs around the top of the barrier since higher energy electrons have higher injection probability in general. This is the situation near the drain when VGS is high and also VDS is high. This "hot electron injection" is being exploited as the programming mechanism in the FLASH memory devices.
As for the injection probability, several physical phenomena are included together into P(x,E) due to the essentially unknown properties of the band structure at the interface and thus hard to distinguish them[1]. These sometimes include emission from Si to SiO2, transport within the SiO2 conduction band, and also tunneling through the SiO2 barrier as well.
The gate current, IG, is the macroscopic way of revealing this injection current in the MOSFET. However, relating the IG with the injection current density is quite complex due to i) reflection back to the Si form SiO2 ii) contribution from holes. In this respect, the IG is in general modeled as:

where W is the width and L is the length of the gate, ηn(x) and ηF(x) are the efficiency that the injected carriers actually reach the gate. Both J and η are the function of position and the bias condition. The Fig. 2 shows an example of calculated IG using this model.
© 2007 Byoungil Lee. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
[1] P. Cappelletti, C. Golla, P. Olivo, and E. Zanoni, Flash Memories, (Kluwer, 1999).
[2] K. Sakui et al., "The Effects of Impact Ionization on the Operation of Neighboring Devices and Circuits", IEEE Trans. Elec. Dev. 41, 1603 (1994).
[3] D. Esseni et al., "Bias and Temperature Dependence of Gate and Substrate Current in n-MOSFETs at Low Drain Voltage", IEDM Tech. Digest, p. 307., (1994).
[4] Hitachi Semiconductor Reliability Handbook.
[5] C. Fiegna et al., "Simple and Efficient Modeling of EPROM Writing", IEEE Trans. Elec. Dev. 38, 603 (1991).
[6] K. Hasnat et al., "Thermionic Emission Model of Electron Gate Current in Submicron n-MOSFETs", IEEE Trans. Elec. Dev. 44, 129 (1997).
[7] P. Cappelletti, et al., "Failure Mechanism of Flash Cell in Program/Erase Cycling", IEDM Tech. Digest, p. 293, (1994).