The Scaling Theory of Localization in Experiment, Part I: Phosphorus-Doped Silicon

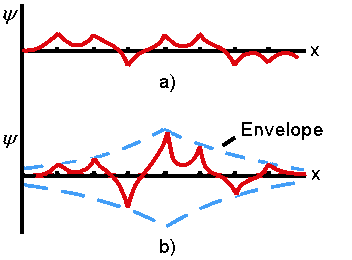
Figure 1: Representations of the electron wavefunction in the Anderson model for a) extended and b) weakly localized cases. [3]

It is well known in theory that bands of electrons of certain energies propagate perfectly through perfect crystals; however, in reality a perfect crystal is a myth. All crystals contain disorder, in the form of impurities, lattice defects, or fluctuations of atomic position due to finite temperature. This report will briefly and qualitatively introduce the scaling theory of localization, which has been very successful at explaining basic phenomena of conductance and magnetoresistance in disordered conductors. It will also review the first important experimental evidence gathered in support of this theory, namely the observation at low temperatures of a metal-to-insulator transition to very low conductivities in a three-dimensional sample of silicon doped with phosphorus.¹

Prior to 1958 the traditional view had been that disorder-induced scattering in a metal causes an electron to lose phase coherence after propagating a distance on the order of its mean free path l, but nevertheless the fundamentally extended state of the electron is preserved. Anderson in 1958 argued that this is not the case; rather, for some critical disorder the electrons become localized in the metal, after which conduction, if it occurs, does so by hopping from localized state to localized state. Crossing this critical disorder threshold marks a fundamental transition from metal to insulator.² A graphical illustration of this transition is shown in Figure 1. Since then a number of theories have attempted to further quantify this metal-insulator transition. One particularly important one by Mott³ predicted a discontinuous metal-insulator transition and a finite minimum conductivity at zero temperature proportional to the interelectronic spacing in a sample. This theory was based in part on the criterion that an electron's mean free path must exceed the distance between atoms.

In contrast, Abrahams et. al. introduced the scaling theory of localization in 1979.⁴ The theory basically models a disordered system as a d-dimensional hypercube, made by putting small cubes of side length L>>l together into a sample of size (2L)^d. The eigenstates of the final sample are linear combinations of the eigenstates of each L^d block. If the eigenstates are mainly localized, they will be insensitive to the boundary conditions used for putting the smaller blocks together; if extended, the opposite. Sensitivity to changing the boundary conditions from periodic to antiperiodic, therefore, is correlated with the nature of the eigenstates as the system gets larger. The crucial hypothesis is that the (dimensionless) conductance g of the system at scale L is directly proportional to and completely characterizes the average of the energy-level differences obtained by modifying the boundary conditions, small for localized systems and larger for extended systems.^4,5,6

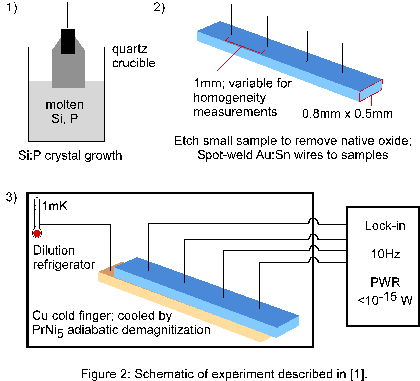Figure 2: Schematic of experiment described in [1].

Abrahams et. al. further argued that since the change in disorder when the system becomes a little bigger is determined by its value at the previous length scale, with the only reasonable measure of this disorder being the conductance, the logarithmic derivative

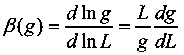
called the scaling parameter, is a monotonic function of g alone. β(g)=0 corresponds to the transition between extended and localized states. In contrast with the previous theory of Mott, for a given sample g is expected to evolve smoothly - with no discontinuity - from a microscopic conductance g₀ to its asymptotic form for large L. This asymptotic form will in general depend on L, the dimensionality of the system, and on the amount of system disorder. In the low scattering limit where Ohm’s law for a d-dimensional hypercube, g(L)=σL^d-2, is valid with no further correction, clearly β(g)=(d-2), implying d=2 is a critical dimension, and that in 2D or below, only localized behavior is possible at large enough length scales.⁴

For large g, it is possible to calculate corrections to the classical β(g)=(d-2) in g^-1 using diagrammatic perturbation theory.^5,7 The first order correction, proportional to g^-1, is found to be negative, i.e., –a/g. Its origin is singular backscattering, which is interference between electron waves and their scattered analogues traveling across time-reversed paths. The Green's function describing propagation of an electron can be constructed as a path integral over all paths connecting the start and endpoints. In the presence of impurities (but no magnetic field) most electrons will arrive at the endpoint with random phase, with the exception of self-intersecting paths. The closed loop in such paths may be traversed in either direction, and so in the presence of time-reversal symmetry the paths will interfere. This interference further localizes the states leading to a first order correction that decreases the value of β(g).

In three dimensions, β(g)=(1-a/g) so the conductance of any disordered system is always less than ohmic. The behavior of a given system will be metallic if its microscopic conductance (its conductance on the length scale l) g₀ > g_c , where g_c is the microscopic conductance for which β(g)=0. Conversely the system will be insulating if g₀ < g_c. Since current in a sample is transported by electrons at the Fermi energy, g₀ is the conductance at this energy. If disorder is kept fixed and instead the Fermi energy is varied, g₀ will change smoothly and will become g_c when the Fermi energy reaches a value defined as the mobility edge. For values near the mobility edge, β(g) may be approximated as linear, or β(g) ≈ δ(g)/v. Then, integrating, g(L)=σL, where σ=g_c/R, is the macroscopic conductivity at the phase transition. R, with units of length, is in this notation

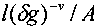
with A a constant of order unity. Note R goes to zero at the phase transition. Extrapolated from an analysis in 2+ε dimensions with ε small, v in 3 dimensions is roughly unity, and it should be the same on either side of the critical point.⁵ In sum, at the mobility edge and at temperatures approaching 0K, the scaling theory of localization predicts a continuous transition to zero of the macroscopic conductivity from some finite value. This is inconsistent with Mott's theory both in the continuity of the transition and in the existence of a finite minimum conductivity.

Using modern semiconductor process technology, it is straightforward to modify the Fermi level of a highly crystalline semiconductor with great accuracy, by doping. Doping in this context is the process of replacing the primary atom at a few lattice sites in the crystal with an atom containing typically one more or one fewer valence electrons. The excess electrons or holes introduced into the crystal via this process modify the density of states in the crystal and shift the Fermi level up or down respectively.⁸ Measurement of the conductivity of semiconductors doped to span the metal-to-insulator transition, at a temperature low enough that the effects of thermal disorder are negligible by comparison, should therefore provide a rigorous test of the scaling theory of localization and the behavior it predicts for the macroscopic conductivity in this regime.

In 1980, Rosenbaum et al. performed just such an experiment with an array of samples of silicon doped with phosphorus (an electron donor).¹ The silicon crystals themselves were grown via a Czochralski process, in which a seed silicon crystal is dipped into molten, ultrahigh purity silicon with the relevant concentration of dopant added, and drawn out under very controlled conditions to produce a crystalline ingot.⁹ The donor density n in the samples was varied from about 3.76x10¹⁸ to about 7x10¹⁸ atoms per cubic centimeter. Resistances were measured using four probes, to minimize the effect of contact resistance; a lock-in amplifier; and a frequency of 10 Hz, to enable phase coherence of voltage and current. Moveable probes were used to ensure homogeneity in n over the relevant length scale. Measurements were obtained at temperatures down to 1 mK using a dilution refrigerator, with the samples attached to a copper cold finger, and the 0K behavior was extrapolated from this data. Further experimental details are shown in the schematic in Figure 2, and a semilog plot of the resulting conductivity obtained as a function of n is shown in Figure 3.¹

The results in Figure 3 show a change of 10³ in the zero-T conductivity for a 1% change in doping density. The transition is sufficiently sharp that its continuity cannot be determined within experimental error. However, the minimum conductivity anticipated by Mott et. al., for the system in question is approximately 20 (ohm cm)^-1, and three metallic samples in the experiment have conductivities significantly lower than this. While density inhomogeneities could, according to the Mott theory, account for the depressed minimum conductivity, it is unlikely they do in this case based on experimental estimations of macroscopic inhomogeneity of ~0.04%.

Figure 3: Semilog plot of zero-temperature conductivity vs. donor density n for metallic samples of Si:P. The solid line is a fit of the form predicted by the the 3D scaling theory of localization, with v = 0.55. [1]

Further, for n farther away from the phase transition, the data fits reasonably well with the result from 3D scaling localization theory. The conductivity in the form σ=g_c/R as obtained from the theory above, fits with

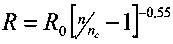
where n_c=3.74x10¹⁸ cm^-3 and g_c/R₀=260 (ohm cm)^-1. The value obtained for v, 0.55, is inconsistent with theory. However it is found to be the same on either side of the transition, using dielectric susceptibility data from insulating samples from a previous experiment.¹⁰ Thus the work in [1] serves as convincing evidence in favor of localization theory in general, and as compelling evidence in favor of a scaling theory of localization in particular.

Neither the Mott theory nor the scaling theory of localization fully explain the dynamics of metal-insulator transitions in imperfect crystals. A more detailed review of subsequent experiments investigating metal-insulator transitions in phosphorus-doped silicon specifically, including the effects of fine-tuning n_c by applying mechanical stress, may be found in [11]. Indeed a good deal of controversy has developed and much has been written on the subject since these initial theories were proposed and experiments performed.^12-14 In particular, the scaling theory discussed in this work has made a number of assumptions, for example that T=0, and that the electrons in the system are noninteracting and in a static random lattice. Some of the most important corrections to the theory presented here are those that introduce effects of temperature and especially Couloumb interactions between electrons.¹³ Further investigations have made predictions for the effect of electric and magnetic fields on disordered conductors. The scaling theory of localization and its derivatives remain highly influential in modern solid state physics and electronics to this day.

© 2007 S.L. Hellstrom. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.

References

[1] T.F. Rosenbaum, K. Andres, G.A. Thomas, R.N. Bhatt, "Sharp Metal-Insulator Transition in a Random Solid," Phys. Rev. Lett. 45, 1723 (1980).

[2] P.W. Anderson, "Absence of Diffusion in Certain Random Lattices," Phys. Rev. 109, 1492 (1958).

[3] N.F. Mott, E.A. Davis, Electronic Processes in Non-Crystalline Materials, (Oxford, 1971).

[4] E. Abrahams, P.W. Anderson, D.C. Licciardello, T.V. Ramakrishnan, "Scaling Theory of Localization: Absence of Quantum Diffusion in Two Dimensions," Phys. Rev. Lett. 42, 673 (1979).

[5] P.A. Lee, T.V. Ramakrishnan, "Disordered Electronic Systems," Rev. Modern Phys. 57, 287 (1985).

[6] D.J. Thouless, "Electrons in Disordered Systems and the Theory of Localization," Phys. Rep. 13C, 93 (1974).

[7] J.S. Langer, T. Neal, "Breakdown of the Concentration Expansion for the Impurity Resistivity of Metals," Phys. Rev. Lett. 16, 984 (1966).

[8] R.S. Muller, T.I. Kamins, M. Chan, Device Electronics for Integrated Circuits, 3^rd Ed., (Wiley, 2003).

[9] J.H. Wang, "Quality Evaluation of Resistivity-Controlled Silicon Crystals," J. Cryst. Growth 287, 258 (2006).

[10] M. Capizzi, G.A. Thomas, F. DeRosa, R.N. Bhatt, T.M. Rice, "Observation of the Approach to a Polarization Catastrophe," Phys. Rev. Lett. 44, 1019 (1980).

[11] T.F. Rosenbaum, R.F. Milligan, M.A. Paalanen, G.A. Thomas, R.N. Bhatt, "Metal-insulator Transition in a Doped Semiconductor," Phys. Rev. B. 27, 7509 (1983).

[12] N.F. Mott, "The Minimum Metallic Conductivity in Three Dimensions," Phil. Mag. B. 44, 265 (1981).

[13] B.L. Altshuler, A.G. Aranov, P.A. Lee, "Interaction Effects in Disordered Fermi Systems in Two Dimensions," Phys. Rev. Lett. 44, 1288 (1980.

[14] B.L. Altshuler, D. Khmel'nitzkii, A.I. Larkin, P.A. Lee, "Magnetoresistance and Hall Effect in a Disordered Two-Dimension Electron Gas," Phys. Rev. B. 22, 5142 (1980).